
【题目】已知二次函数![]() (
(![]() ),
),![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
|
| -1 | 0 | 1 | 2 | 3 | 4 |
|
|
| 6 | 1 | -2 | -3 | -2 |
|
|
下面有四个论断:①抛物线![]() (
(![]() )的顶点为
)的顶点为![]() ;②
;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 的解为
的解为![]() ,
,![]() ;④当
;④当![]() 时,
时,![]() 的值为正,其中正确的有_______.
的值为正,其中正确的有_______.
【答案】①③④
【解析】
根据表格,即可判断出抛物线的对称轴,从而得到顶点坐标,即可判断①;根据抛物线的对称性即可判断②;根据表格中函数值为-2时,对应的x的值,即可判断③;根据二次函数的增减性即可判断④.
解:①根据表格可知:抛物线![]() (
(![]() )的对称轴为x=2,
)的对称轴为x=2,
∴抛物线![]() (
(![]() )的顶点为
)的顶点为![]() ,故①正确;
,故①正确;
②根据抛物线的对称性可知:当x=4和x=0时,对应的函数值相同,
∴m=1,故②错误;
③由表格可知:对于二次函数![]() ,当y=-2时,对应的x的值为1或3
,当y=-2时,对应的x的值为1或3
∴关于![]() 的方程
的方程![]() 的解为
的解为![]() ,
,![]() ,故③正确;
,故③正确;
④由表格可知:当x<2时,y随x的增大而减小
∵![]() ,抛物线过(0,1)
,抛物线过(0,1)
∴当![]() 时,
时,![]() >1>0
>1>0
∴当![]() 时,
时,![]() 的值为正,故④正确.
的值为正,故④正确.
故答案为:①③④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
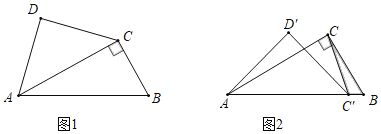
【题目】一副三角板如图1放置(有一条边重合),如图2把含45°的直角三角板ACD绕点A顺时针旋转30°,得到△AC′D′,若BC=2,则△BCC′的面积为( )
A.2![]() ﹣3B.3﹣
﹣3B.3﹣![]() C.4
C.4![]() ﹣6D.6﹣2
﹣6D.6﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
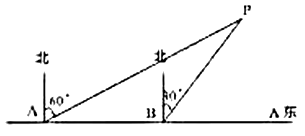
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等
(1)若从中只录用一人,恰好选到思政专业毕业生的概率是 :
(2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() .抛物线的解析式为
.抛物线的解析式为![]() .
.
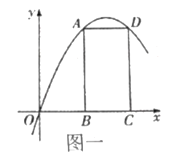
(1)如图一,若抛物线经过![]() ,
,![]() 两点,直接写出
两点,直接写出![]() 点的坐标 ;抛物线的对称轴为直线 ;
点的坐标 ;抛物线的对称轴为直线 ;
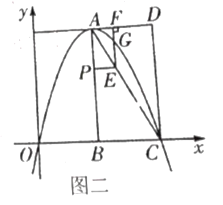
(2)如图二:若抛物线经过![]() 、
、![]() 两点,
两点,
①求抛物线的表达式.
②若点![]() 为线段
为线段![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() 交抛物线于点
交抛物线于点![]() .当线段
.当线段![]() 最长时,求点
最长时,求点![]() 的坐标;
的坐标;
(3)若![]() ,且抛物线与矩形
,且抛物线与矩形![]() 没有公共点,直接写出
没有公共点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
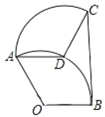
【题目】如图,将半径为1,圆心角为120°的扇形OAB绕点A逆时针旋转一个角度,使点O的对应点D落在弧AB上,点B的对应点为C,连接BC,则图中CD、BC和弧BD围成的封闭图形面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
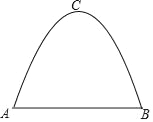
【题目】一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
查看答案和解析>>
科目:初中数学 来源: 题型:
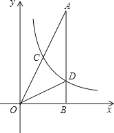
【题目】如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
(1)求反比例函数解析式;
(2)将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com