

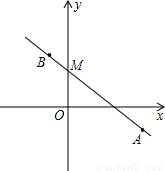
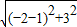 =3
=3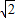 ;
; =
=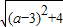 ,
,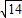 ,
,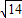 ,0);
,0);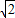 时,
时,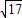 ,0);
,0); AD•BE=
AD•BE= ×6×4=12,
×6×4=12, =
=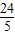 ,12×
,12× =
=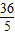 ,
, ×4×(2+b)=
×4×(2+b)= ,
, ,
, )代入y=-x+1得,a=
)代入y=-x+1得,a= ,
, ,
, ),
),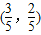 或F
或F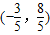 ,
, DE•BE=4<12×
DE•BE=4<12× =
=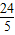 ,故这种情况不存在.
,故这种情况不存在.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源:2006年山西省太原市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年山西省太原市中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年山西省太原市中考数学试卷(解析版) 题型:选择题
 的中点,∠OAB=40°,则∠BOC等于( )
的中点,∠OAB=40°,则∠BOC等于( )
查看答案和解析>>
科目:初中数学 来源:2006年山西省太原市中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com