

| A. | ②③④ | B. | ①②③ | C. | ①③④ | D. | ①②④ |
分析 由图2可知,在点(10,40)至点(14,40)区间,△BPQ的面积不变,因此可推论BC=BE,由此分析动点P的运动过程如下:
(1)在BE段,BP=BQ;持续时间10s,则BE=BC=10;y是t的二次函数;
(2)在ED段,y=40是定值,持续时间4s,则ED=4;
(3)在DC段,y持续减小直至为0,y是t的一次函数.
解答  解:(1)分析函数图象可知,BC=10cm,ED=4cm,故AE=AD-ED=BC-ED=10-4=6cm,故①正确;
解:(1)分析函数图象可知,BC=10cm,ED=4cm,故AE=AD-ED=BC-ED=10-4=6cm,故①正确;
(2)如答图1所示,连接EC,过点E作EF⊥BC于点F,
由函数图象可知,BC=BE=10cm,S△BEC=40=$\frac{1}{2}$BC•EF=$\frac{1}{2}$×10×EF,∴EF=8,
∴sin∠EBC=$\frac{EF}{BE}=\frac{8}{10}=\frac{4}{5}$,故②正确;
(3)如答图2所示,过点P作PG⊥BQ于点G,
∵BQ=BP=t,
∴y=S△BPQ=$\frac{1}{2}$BQ•PG=$\frac{1}{2}$BQ•BP•sin∠EBC=$\frac{1}{2}$t•t•$\frac{4}{5}$=$\frac{2}{5}$t2.
故③正确;
(4)结论D错误.理由如下:
当t=12s时,点Q与点C重合,点P运动到ED的中点,设为N,如答图3所示,连接NB,NC.
此时AN=8,ND=2,由勾股定理求得:NB=8$\sqrt{2}$,NC=2$\sqrt{17}$,
∵BC=10,
∴△BCN不是等腰三角形,即此时△PBQ不是等腰三角形.
故④错误;
正确的结论有:①②③.
故选:B.
点评 本题考查动点问题的函数图象,需要结合几何图形与函数图象,认真分析动点的运动过程.突破点在于正确判断出BC=BE=10cm.


科目:初中数学 来源: 题型:选择题
| A. | 垂线段最短 | |
| B. | 对顶角相等 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$,-1) | B. | (-1,$\sqrt{3}$) | C. | (-$\sqrt{3}$,1) | D. | (1,-$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=35°,则∠B的度数是( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
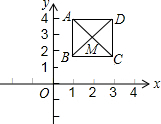 如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).
如图,已知正方形ABCD,顶点A(1,4),B(1,2),C(3,2),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标为(2017,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
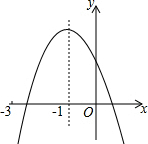 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )| A. | ①③④ | B. | ①②④⑤ | C. | ②③⑤ | D. | ①③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
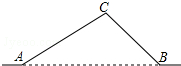 如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.
如图,从城市A到B城市的公路需经过城市C,图中AC=100千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两城市间修建一条笔直的公路.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com