
分析 在Rt△ADA′中,由勾股定理求得AA′的长度,然后再证明△NOA′∽△ADA′,利用相似三角形的性质可得到$\frac{A′N}{AA′}=\frac{OA′}{DA′}$,从而可求得A′N=4.1,DN=A′D-A′N=5-4.1=0.9.
解答 解:根据题意画出图形.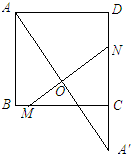
在Rt△ADA′中,AA′=$\sqrt{A{D}^{2}+DA{′}^{2}}=\sqrt{{4}^{2}+{5}^{2}}=\sqrt{41}$,
由轴对称的性质可知:OA=OA′=$\frac{1}{2}AA′$=$\frac{\sqrt{41}}{2}$,
在△NOA′和△ADA′中,∠D=∠NOA′,∠A=∠A′,
∴△NOA′∽△ADA′.
∴$\frac{A′N}{AA′}=\frac{OA′}{DA′}$.
∴$\frac{A′N}{\sqrt{41}}=\frac{\frac{\sqrt{41}}{2}}{5}$.
∴A′N=4.1
∴DN=A′D-A′N=5-4.1=0.9.
故答案为:0.9.
点评 本题主要考查的是相似三角形的性质和判定、勾股定理和轴对称性质的应用,利用相似三角形的性质求得A′N的长度是解题的关键.


科目:初中数学 来源: 题型:选择题

| A. | ②③④ | B. | ①②③ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
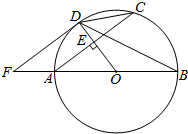 如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.
如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
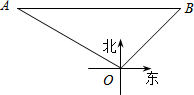 在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.
在海上某固定观测点O处的北偏西60°方向,且距离O处40海里的A处,有一艘货轮正沿着正东方向匀速航行,2小时后,此货轮到达O处的北偏东45°方向的B处.在该货轮从A处到B处的航行过程中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
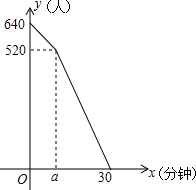 汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:
汛期来临,水库水位不断上涨,经勘测发现,水库现在超过警戒线水量640万米3,设水流入水库的速度是固定的,每个泄洪闸速度也是固定的,泄洪时,每小时流入水库的水量16万米3,每小时每个泄洪闸泄洪14万米3,已知泄洪的前a小时只打开了两个泄洪闸,水库超过警戒线的水量y(万米3)与泄洪时间s(小时)的关系如图所示,根据图象解答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 海拔/米 | 0 | 100 | 200 | 300 | 400 | … |
| 平均气温/℃ | 24 | 23.4 | 22.8 | 22.2 | 21.6 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
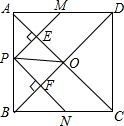 如图,在正方形ABCD中,点P是AB边上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF.其中正确的结论有3个.
如图,在正方形ABCD中,点P是AB边上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF.其中正确的结论有3个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
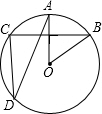 如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=50°,则∠ADC的度数是( )
如图,在⊙O中,$\widehat{AB}$=$\widehat{AC}$,∠AOB=50°,则∠ADC的度数是( )| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com