
【题目】如图,在数轴上有两点A、B,点A表示的数是8,点B在点A的左侧,且AB=14,动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.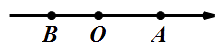
(1)写出数轴上点B表示的数: ;点P表示的数用含t的代数式表示为 .
(2)动点Q从点B出发沿数轴向左匀速运动,速度是点P速度的一半,动点P、Q同时出发,问点P运动多少秒后与点Q的距离为2个单位?
(3)若点M为线段AP的中点,点N为线段BP的中点,在点P的运动过程中,线段MN的长度是否会发生变化?若变化,请说明理由;若不变,求出线段MN的长.
【答案】
(1)解:8-14=-6;因此B点为-6;故答案为:-6,解:因为时间为t,则点P所移动距离为4t,因此点P为8-4t ;故答案为:8-4t
(2)解:由题意得,Q 的速度为4÷2=2(秒)则点Q为-6-2t,又点P为8-4t;
所以①P在Q的右侧时
8-4t-(-2t-6)=2
解得x=6
②P在Q左侧时
-2t-6-(8-4t)=2
解得x=8
答:动点P、Q同时出发,问点P运动6或8秒后与点Q的距离为2个单位.
故答案为:6或8秒
(3)解:①当P在A,B之间时,线段AP=8-(8-4t)=4t;线段BP=8-4t-(-6)=14-4t
因点M为线段AP的中点,点N为线段BP的中点
所以MP=![]() AP=2t;NP=
AP=2t;NP=![]() BP=7-2t
BP=7-2t
MN=MP+NP=2t+7-2t=7
②当P在P的左边时线段AP=8-(8-4t)=4t;线段BP=(-6)-(8-4t)=4t-14
因点M为线段AP的中点,点N为线段BP的中点
所以MP=![]() AP=2t;NP=
AP=2t;NP=![]() BP=2t-7
BP=2t-7
MN=MP-NP=2t-(2t-7)=7
因此在点P的运动过程中,线段MN的长度不变, MN=7
【解析】(1)①由数轴上两点之间距离的规律易得B的值为8-14=16;
②因为时间为t,则点P所移动距离为4t,因此易得P为8-4t
(2)由题易得:Q 的速度为4÷2=2(秒)则点Q为-6-2t,又点P为8-4t;分别讨论P在Q左侧或右侧的情况,由此列方程,易得结果为6或8秒;
(3)结合(1)(2)易得当P在AB间以及P在B左边时的两种情况;当P在A,B之间时,线段AP=8-(8-4t)=4t;线段BP=8-4t-(-6)=14-4t;当P在P的左边时线段AP=8-(8-4t)=4t;线段BP=(-6)-(8-4t)=4t-14;利用中点性质,易得结果不变,为7.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
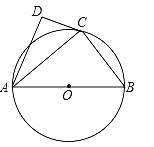
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为千米;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com