
ЁОЬтФПЁПвбжЊЃКдкЁїABCжаЃЌABЃНACЃЌЕуDЮЊBCБпЕФжаЕуЃЌЕуFЪЧABБпЩЯвЛЕуЃЌЕуEдкЯпЖЮDFЕФбгГЄЯпЩЯЃЌЁЯBAEЃНЁЯBDFЃЌЕуMдкЯпЖЮDFЩЯЃЌЁЯABE=ЁЯDBMЃЎ

ЃЈ1ЃЉШчЭМ1ЃЌЕБЁЯABCЃН45ЁуЪБЃЌЧѓжЄЃКAEЃН![]() MDЃЛ
MDЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЁЯABCЃН60ЁуЪБЃЌ
ЂйжБНгаДГіЯпЖЮAEЃЌMDжЎМфЕФЪ§СПЙиЯЕЃЛ
ЂкбгГЄBMЕНPЃЌЪЙMPЃНBMЃЌСЌНгCPЃЌШєABЃН7ЃЌAEЃН![]() ЃЌЬНЧѓsinЁЯPCBЕФжЕЃЎ
ЃЌЬНЧѓsinЁЯPCBЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЂйAEЃН2DMЃЌРэгЩМћНтЮіЃЛЂк![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтжЊЁЯBAEЃНЁЯBDMЃЌЁЯABEЃНЁЯDBMЙЪгаЁїABEЁзЁїDBMЃЌДгЖјЕУЕНAEЃКDMЃНABЃКBDЃЌЖјЁЯABCЃН45ЁуЃЌдйЕУЕНABЃН![]() BDЃЌдђгаAEЃН
BDЃЌдђгаAEЃН![]() MDЃЛ
MDЃЛ
ЃЈ2ЃЉЂйгЩгкЁїABEЁзЁїDBMЃЌЯрЫЦБШЮЊ2ЃЌЙЪгаEBЃН2BMЃЌНјЖјШЗЖЈГіAEгыDMЕФЙиЯЕЃЛ
ЂкгЩЬтвтжЊЕУЁїBEPЮЊЕШБпШ§НЧаЮЃЌгаEMЁЭBPЃЌЁЯBMDЃНЁЯAEBЃН90ЁуЃЌдкRtЁїAEBжаЧѓЕУAEЁЂABЁЂtanЁЯEABЕФжЕЃЌгЩDЮЊBCжаЕуЃЌMЮЊBPжаЕуЃЌЕУDMЁЮPCЃЌЧѓЕУtanЁЯPCBЕФжЕЃЌдкRtЁїABDКЭRtЁїNDCжаЃЌгЩШёНЧШ§НЧКЏЪ§ЕФЖЈвхЧѓЕУADЁЂNDЕФжЕЃЌНјЖјЧѓЕУtanЁЯPCBЕФжЕЃЎ
ЃЈ1ЃЉжЄУїЃКШчЭМ1ЃЌСЌНгADЃЎ
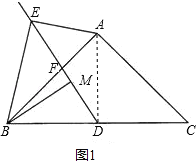
ЁпABЃНACЃЌBDЃНCDЃЌ
ЁрADЁЭBCЃЎ
гжЁпЁЯABCЃН45ЁуЃЌ
ЁрBDЃНABcosЁЯABCЃЌМДABЃН![]() BDЃЎ
BDЃЎ
ЁпЁЯBAEЃНЁЯBDMЃЌЁЯABEЃНЁЯDBMЃЌ
ЁрЁїABEЁзЁїDBMЃЎ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрAEЃН![]() MDЃЎ
MDЃЎ
ЃЈ2ЃЉЂйШчЭМ2ЃЌСЌНгADЃЌEPЃЌЙ§NзїNHЁЭACЃЌДЙзуЮЊHЃЌСЌНгNHЃЌ
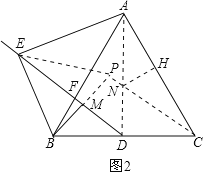
ЁпABЃНACЃЌЁЯABCЃН60ЁуЃЌ
ЁрЁїABCЪЧЕШБпШ§НЧаЮЃЌ
гжЁпDЮЊBCЕФжаЕуЃЌ
ЁрADЁЭBCЃЌЁЯDACЃН30ЁуЃЌBDЃНDCЃН![]() ABЃЌ
ABЃЌ
ЁпЁЯBAEЃНЁЯBDMЃЌЁЯABEЃНЁЯDBMЃЌ
ЁрЁїABEЁзЁїDBMЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃН2ЃЌЁЯAEBЃНЁЯDMBЃЌМДAEЃН2DMЃЛ
ЃН2ЃЌЁЯAEBЃНЁЯDMBЃЌМДAEЃН2DMЃЛ
ЂкЁпЁїABEЁзЁїDBMЃЌ
Ёр![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃН2ЃЌ
ЃН2ЃЌ
ЁрEBЃН2BMЃЌ
гжЁпBMЃНMPЃЌ
ЁрEBЃНBPЃЌ
ЁпЁЯEBMЃНЁЯEBA+ЁЯABMЃНЁЯMBD+ЁЯABMЃНЁЯABCЃН60ЁуЃЌ
ЁрЁїBEPЮЊЕШБпШ§НЧаЮЃЌ
ЁрEMЁЭBPЃЌ
ЁрЁЯBMDЃН90ЁуЃЌ
ЁрЁЯAEBЃН90ЁуЃЌ
дкRtЁїAEBжаЃЌAEЃН2![]() ЃЌABЃН7ЃЌ
ЃЌABЃН7ЃЌ
ЁрBEЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрtanЁЯEABЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпDЮЊBCжаЕуЃЌMЮЊBPжаЕуЃЌ
ЁрDMЁЮPCЃЌ
ЁрЁЯMDBЃНЁЯPCBЃЌ
ЁрЁЯEABЃНЁЯPCBЃЌ
ЁрtanЁЯPCBЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧдјбЇЙ§ЖЈРэЁАдкжБНЧШ§НЧаЮжаЃЌШчЙћвЛИіШёНЧЕШгк![]() ЃЌФЧУДЫќЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЁБЃЌЦфФцУќЬтвВЪЧГЩСЂЕФЃЌМДЁАдкжБНЧШ§НЧаЮжаЃЌШчЙћвЛжБНЧБпЕШгкаББпЕФвЛАыЃЌФЧУДИУжБНЧБпЫљЖдЕФНЧЮЊ
ЃЌФЧУДЫќЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЁБЃЌЦфФцУќЬтвВЪЧГЩСЂЕФЃЌМДЁАдкжБНЧШ§НЧаЮжаЃЌШчЙћвЛжБНЧБпЕШгкаББпЕФвЛАыЃЌФЧУДИУжБНЧБпЫљЖдЕФНЧЮЊ![]() ЁБ.ШчЭМЃЌдк
ЁБ.ШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌШчЙћ
ЃЌШчЙћ![]() ЃЌФЧУД
ЃЌФЧУД![]() .
.
ЧыФуИљОнЩЯЪіУќЬтЃЌНтОіЯТУцЕФЮЪЬтЃК

ЃЈ1ЃЉШчЭМ1ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊИёЕуЃЌвд
ЮЊИёЕуЃЌвд![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ГЄЮЊАыОЖЛЛЁНЛжБЯп
ГЄЮЊАыОЖЛЛЁНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌдђ
ЃЌдђ![]() ______
______![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌ![]() ЁЂ
ЁЂ![]() ЮЊИёЕуЃЌАДвЊЧѓдкЭјИёжазїЭМЃЈБЃСєзїЭМКлМЃЃЉЁЃ
ЮЊИёЕуЃЌАДвЊЧѓдкЭјИёжазїЭМЃЈБЃСєзїЭМКлМЃЃЉЁЃ
зї![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌВЂЧв
ЩЯЃЌВЂЧв![]() ЃЌ
ЃЌ![]() .
.
ЃЈ3ЃЉШчЭМ3ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ФквЛЕуЃЌ
ФквЛЕуЃЌ![]() ЃЌ
ЃЌ![]() гк
гк![]() ЃЌЧв
ЃЌЧв![]() .
.
ЂйЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЂкЧѓжЄЃК![]() .
.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЧњЯп![]() ЪЧХзЮяЯп
ЪЧХзЮяЯп![]() ЕФвЛВПЗжЃЈЦфжа
ЕФвЛВПЗжЃЈЦфжа![]() ЪЧХзЮяЯпгы
ЪЧХзЮяЯпгы![]() жсЕФНЛЕуЃЌ
жсЕФНЛЕуЃЌ![]() ЪЧЖЅЕуЃЉЃЌЧњЯп
ЪЧЖЅЕуЃЉЃЌЧњЯп![]() ЪЧЫЋЧњЯп
ЪЧЫЋЧњЯп![]() ЕФвЛВПЗжЃЎЧњЯп
ЕФвЛВПЗжЃЎЧњЯп![]() гы
гы![]() зщГЩЭМаЮ
зщГЩЭМаЮ![]() ЃЎгЩЕу
ЃЎгЩЕу![]() ПЊЪМВЛЖЯжиИДЭМаЮ
ПЊЪМВЛЖЯжиИДЭМаЮ![]() аЮГЩвЛзщЁАВЈРЫЯпЁБЃЎШєЕу
аЮГЩвЛзщЁАВЈРЫЯпЁБЃЎШєЕу![]() ЃЌ
ЃЌ![]() дкИУЁАВЈРЫЯпЁБЩЯЃЌдђ
дкИУЁАВЈРЫЯпЁБЩЯЃЌдђ![]() ЕФзюДѓжЕЮЊЃЈ ЃЉ
ЕФзюДѓжЕЮЊЃЈ ЃЉ
A.5B.6C.2020D.2021
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
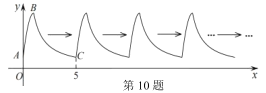
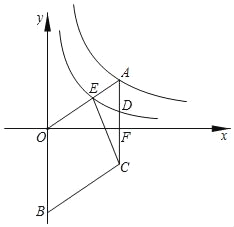
ЁОЬтФПЁПШчЭМЫљЪОЃЌСтаЮAOBCЕФЖЅЕуBдкyжсЩЯЃЌЖЅЕуAдкЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЩЯЃЌБпACЃЌOAЗжБ№НЛЗДБШР§КЏЪ§yЃН
ЕФЭМЯѓЩЯЃЌБпACЃЌOAЗжБ№НЛЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓгкЕуDЃЌЕуEЃЌБпACНЛxжсгкЕуFЃЌСЌНгCEЃЎвбжЊЫФБпаЮOBCEЕФУцЛ§ЮЊ12ЃЌsinЁЯAOFЃН
ЕФЭМЯѓгкЕуDЃЌЕуEЃЌБпACНЛxжсгкЕуFЃЌСЌНгCEЃЎвбжЊЫФБпаЮOBCEЕФУцЛ§ЮЊ12ЃЌsinЁЯAOFЃН![]() ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЃЌдђkЕФжЕЮЊЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
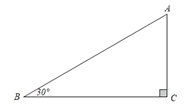
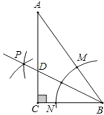
ЁОЬтФПЁПШчЭМЃЌдкRtABCжаЃЌЁЯCЃН90ЁуЃЌвдЖЅЕуBЮЊдВаФЃЌЪЪЕБГЄЖШЮЊАыОЖЛЛЁЃЌЗжБ№НЛABЃЌBCгкЕуMЃЌNЃЌдйЗжБ№вдЕуMЃЌNЮЊдВаФЃЌДѓгк![]() ЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌзїЩфЯпBPНЛACгкЕуDЃЎЕБЁЯAЃН30ЁуЪБЃЌаЁУєе§ШЗЧѓЕУ
ЕФГЄЮЊАыОЖЛЛЁЃЌСНЛЁНЛгкЕуPЃЌзїЩфЯпBPНЛACгкЕуDЃЎЕБЁЯAЃН30ЁуЪБЃЌаЁУєе§ШЗЧѓЕУ![]() ЃК
ЃК![]() ЃН1:2ЃЎаДГіСНЬѕаЁУєЧѓНтжагУЕНЕФЪ§бЇвРОнЃК__________________ЃЎ
ЃН1:2ЃЎаДГіСНЬѕаЁУєЧѓНтжагУЕНЕФЪ§бЇвРОнЃК__________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкПЙЛїаТЙкзДВЁЖОеНЖЗжаЃЌга152ЯфЙЋЙВЮРЩњЗРЛЄгУЦЗвЊдЫЕН![]() ЁЂ
ЁЂ![]() СНГЧеђЃЌШєгУДѓаЁЛѕГЕЙВ15СОЃЌдђЧЁКУФмвЛДЮаддЫЭъетХњЗРЛЄгУЦЗЃЌвбжЊетСНжжДѓаЁЛѕГЕЕФдиЛѕФмСІЗжБ№ЮЊ12Яф/СОКЭ8Яф/СОЃЌЦфжагУДѓЛѕГЕдЫЭљ
СНГЧеђЃЌШєгУДѓаЁЛѕГЕЙВ15СОЃЌдђЧЁКУФмвЛДЮаддЫЭъетХњЗРЛЄгУЦЗЃЌвбжЊетСНжжДѓаЁЛѕГЕЕФдиЛѕФмСІЗжБ№ЮЊ12Яф/СОКЭ8Яф/СОЃЌЦфжагУДѓЛѕГЕдЫЭљ![]() ЁЂ
ЁЂ![]() СНГЧеђЕФдЫЗбЗжБ№ЮЊУПСО800дЊКЭ900дЊЃЌгУаЁЛѕГЕдЫЭљ
СНГЧеђЕФдЫЗбЗжБ№ЮЊУПСО800дЊКЭ900дЊЃЌгУаЁЛѕГЕдЫЭљ![]() ЁЂ
ЁЂ![]() СНГЧеђЕФдЫЗбЗжБ№ЮЊУПСО400дЊКЭ600дЊЃЎ
СНГЧеђЕФдЫЗбЗжБ№ЮЊУПСО400дЊКЭ600дЊЃЎ
ЃЈ1ЃЉЧѓет15СОГЕжаДѓаЁЛѕГЕИїЖрЩйСОЃП
ЃЈ2ЃЉЯжАВХХЦфжа10СОЛѕГЕЧАЭљ![]() ГЧеђЃЌЦфгрЛѕГЕЧАЭљ
ГЧеђЃЌЦфгрЛѕГЕЧАЭљ![]() ГЧеђЃЌЩшЧАЭљ
ГЧеђЃЌЩшЧАЭљ![]() ГЧеђЕФДѓЛѕГЕЮЊ
ГЧеђЕФДѓЛѕГЕЮЊ![]() СОЃЌЧАЭљ
СОЃЌЧАЭљ![]() ЁЂ
ЁЂ![]() СНГЧеђзмЗбгУЮЊ
СНГЧеђзмЗбгУЮЊ![]() дЊЃЌЪдЧѓГі
дЊЃЌЪдЧѓГі![]() гы
гы![]() ЕФКЏЪ§НтЮіЪНЃЎШєдЫЭљ
ЕФКЏЪ§НтЮіЪНЃЎШєдЫЭљ![]() ГЧеђЕФЗРЛЄгУЦЗВЛФмЩйгк100ЯфЃЌЧыФуаДГіЗћКЯвЊЧѓЕФзюЩйЗбгУЃЎ
ГЧеђЕФЗРЛЄгУЦЗВЛФмЩйгк100ЯфЃЌЧыФуаДГіЗћКЯвЊЧѓЕФзюЩйЗбгУЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊТњзуЪаГЁашЧѓЃЌФГГЌЪадкЖЫЮчНкЧАЯІЙКНјМлИёЮЊ3дЊ/ИіЕФФГЦЗХЦєезгЃЌИљОнЪаГЁдЄВтЃЌИУЦЗХЦєезгУПИіЪлМл4дЊЪБЃЌУПЬьФмГіЪл500ИіЃЌВЂЧвЪлМлУПЩЯеЧ0.1дЊЃЌЦфЯњЪлСПНЋМѕЩй10ИіЃЎ
(1)ШєУПИієезгЪлМл4.5дЊЃЌдђУПЬьЕФЯњСПЪЧ______ИіЃЛ
(2)ЮЊСЫЮЌЛЄЯћЗбепРћвцЃЌЮяМлВПУХЙцЖЈЃЌИУЦЗХЦєезгЪлМлВЛФмГЌЙ§НјМлЕФ200%ЃЌЧыФуРћгУЫљбЇжЊЪЖАяжњГЌЪаИјИУЦЗХЦєезгЖЈМлЃЌЪЙГЌЪаУПЬьЕФЯњЪлРћШѓЮЊ800дЊЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЮЪЬтЃЉгУnИі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁСnОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃПЃЈ2ЁСnОиаЮБэЪООиаЮЕФСкБпЪЧ2КЭnЃЉ
ЃЈЬНОПЃЉВЛЗСМйЩшгаanжжВЛЭЌЕФЯтЧЖЗНАИЃЎЮЊЬНОПanЕФБфЛЏЙцТЩЃЌЮвУЧВЩШЁвЛАуЮЪЬтЬиЪтЛЏЕФВпТдЃЌЯШДгзюМђЕЅЧщаЮШыЪжЃЌдйж№ДЮЕнНјЃЌзюКѓВТЯыЕУГіНсТлЃЎ
ЬНОПвЛЃКгУ1Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС1ОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
ШчЭМЃЈ1ЃЉЃЌЯдШЛжЛга1жжЯтЧЖЗНАИЃЎЫљвдЃЌa1ЃН1ЃЎ
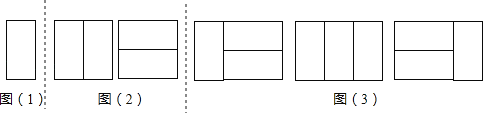
ЬНОПЖўЃКгУ2Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС2ОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
ШчЭМЃЈ2ЃЉЃЌЯдШЛжЛга2жжЯтЧЖЗНАИЃЎЫљвдЃЌa2ЃН2ЃЎ
ЬНОПШ§ЃКгУ3Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС3ОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
вЛРрЃКдкЬНОПвЛУПИіЯтЧЖЭМЕФгвВрдйКсзХЯтЧЖ2Иі2ЁС1ОиаЮЃЌга1жжЯтЧЖЗНАИЃЛ
ЖўРрЃКдкЬНОПЖўУПИіЯтЧЖЭМЕФгвВрдйЪњзХЯтЧЖ1Иі2ЁС1ОиаЮЃЌга2жжЯтЧЖЗНАИЃЛ
ШчЭМЃЈ3ЃЉЃЎЫљвдЃЌa3ЃН1+2ЃН3ЃЎ
ЬНОПЫФЃКгУ4Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС4ОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
вЛРрЃКдкЬНОПЖўУПИіЯтЧЖЭМЕФгвВрдйКсзХЯтЧЖ2Иі2ЁС1ОиаЮЃЌгаЁЁ ЁЁжжЯтЧЖЗНАИЃЛ
ЖўРрЃКдкЬНОПШ§УПИіЯтЧЖЭМЕФгвВрдйЪњзХЯтЧЖ1Иі2ЁС1ОиаЮЃЌгаЁЁ ЁЁжжЯтЧЖЗНАИЃЛ
ЫљвдЃЌa4ЃНЁЁ ЁЁЃЎ
ЬНОПЮхЃКгУ5Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС5ОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
ЃЈЗТееЩЯЪіЗНЗЈЃЌаДГіЬНОПЙ§ГЬЃЌВЛгУЛЭМЃЉ
ЁЁ
ЃЈНсТлЃЉгУnИі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁСnОиаЮЃЌгаЖрЩйжжВЛЭЌЕФЯтЧЖЗНАИЃП
ЃЈжБНгаДГіanгыanЉ1ЃЌanЉ2ЕФЙиЯЕЪНЃЌВЛаДНтД№Й§ГЬЃЉЃЎ
ЃЈгІгУЃЉгУ10Иі2ЁС1ОиаЮЃЌЯтЧЖвЛИі2ЁС10ОиаЮЃЌгаЁЁ ЁЁжжВЛЭЌЕФЯтЧЖЗНАИЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаЮхеХЭъШЋЯрЭЌЕФПЈЦЌЃЌе§УцЗжБ№ЛгаЦНааЫФБпаЮЁЂЕШБпШ§НЧаЮЁЂе§ЮхБпаЮЁЂОиаЮЁЂдВЃЌНЋЫќУЧДђТвЫГађКѓБГУцЯђЩЯЃЌДгжаЫцЛњбЁШЁвЛеХПЈЦЌЃЌе§УцЭМаЮМШЪЧжааФЖдГЦЭМаЮгжЪЧжсЖдГЦЭМаЮЕФИХТЪЮЊ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com