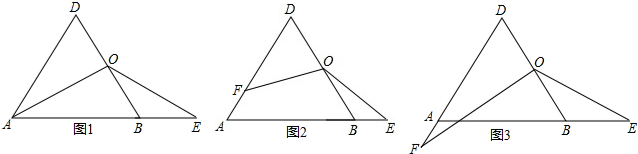
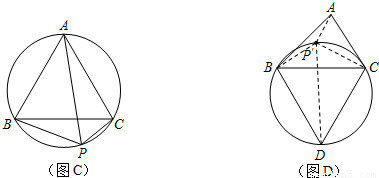(1)证明:∵△ABD是等边三角形,
∴AB=AD=BD.∠DAB=∠ABD=∠D=60°
∵点O是BD的中点,
∴DO=BO=

BD.∠AOD=∠AOB=90°,
∴∠BAO=30°.
设AB=AD=BD=2a,
∴DO=BO=a,
∵∠AOE=120°,
∴∠E=30°,
∴∠BAO=∠E,
∴AO=EO,即FO=EO,
∵AE+AF=3a,AB=2a,
∴AE+AF=

AB.
(2)证明:如图2,过点O作OC∥AB交AD于点C,
∴∠DCO=∠A=∠DCO=∠ABD=60°,
∴∠DOC=60°,∠ACO=∠BOC=120°.
∴△CDO是等边三角形,
∴CO=DO,
∴CO=BO=AC.
∵△ABD是等边三角形,
∴AB=AD=BD.∠DAB=∠ABD=∠D=60°,
∴∠OBE=120°,
∴∠OCF=∠OBE.
∵∠FOB+∠BOE=∠EOF=120°,∠COF+∠FOB=∠BOC=120°
∴∠FOC=∠EOB.
在△COF和△BOE中,

,
∴△COF≌△BOE(ASA).
∴FC=EB.OF=OE.
∵AE+AF=AB+BE+AF,
∴AE+AF=AB+AC
设AB=AD=BD=2a,
∴DO=BO=a,
∴AB+AC=3a,
∴AB+AC=

AB,
∴AE+AF=

AB.
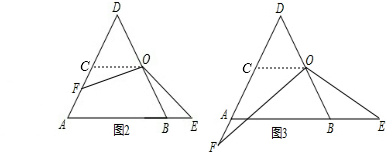
(3)如图3,过点O作OC∥AB交AD于点C,
∴∠DCO=∠A=∠DCO=∠ABD=60°,
∴∠DOC=60°,∠ACO=∠BOC=120°.
∴△CDO是等边三角形,
∴CO=DO,
∴CO=BO=AC.
∵△ABD是等边三角形,
∴AB=AD=BD.∠DAB=∠ABD=∠D=60°,
∴∠OBE=120°,
∴∠OCF=∠OBE.
∵∠FOB+∠BOE=∠EOF=120°,∠COF+∠FOB=∠BOC=120°
∴∠FOC=∠EOB.
在△COF和△BOE中,

,
∴△COF≌△BOE(ASA).
∴FC=EB.OF=OE.
∵AE=AB+BE,
∴AE=AB+CF,
∴AE=AB+AC+AF,
∴AE-AF=AB+AC.
∵AB+AC=

AB,
∴AE-AF=

AB.
故答案为:AE-AF=

AB.
分析:(1)等边△ABD的边长为2a,根据等边三角形的性质就可以求出OD=OB=BE=a,由勾股定理就可以求出OA的值,就可以得出结论;
(2)如图2,过点O作OC∥AB交AD于点C,根据等腰三角形的性质就可以得出△OCF≌△OBE,就可以得出CF=BE,进而可以得出结论;
(3)如图3,过点O作OC∥AB交AD于点C,根据等腰三角形的性质就可以得出△OCF≌△OBE,就可以得出CF=BE,进而可以得出结论.
点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,线段中点的性质的运用,解答时正确作辅助线证明三角形全等是关键.

 AB;
AB;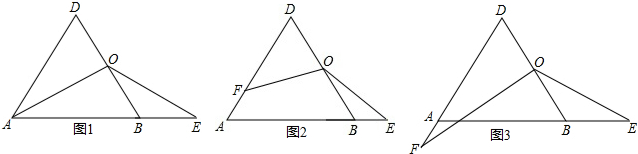
 BD.∠AOD=∠AOB=90°,
BD.∠AOD=∠AOB=90°, AB.
AB. ,
, AB,
AB, AB.
AB.
 ,
, AB,
AB, AB.
AB. AB.
AB.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案


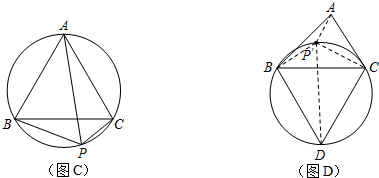
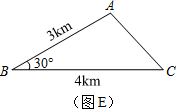
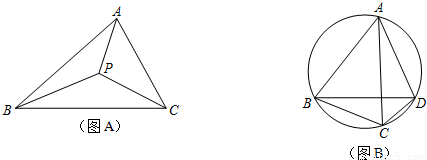
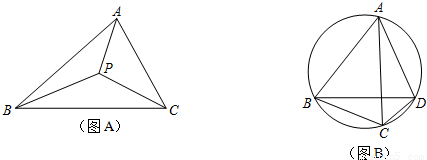
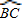 上任意一点.求证:PB+PC=PA;
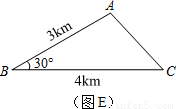
上任意一点.求证:PB+PC=PA;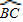 上任取一点P′,连接P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+______;
上任取一点P′,连接P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+______;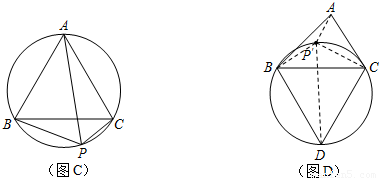
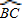 上任意一点.求证:PB+PC=PA;
上任意一点.求证:PB+PC=PA; 上任取一点P′,连接P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+______;
上任取一点P′,连接P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+______;