
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E是AB的中点.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E是AB的中点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
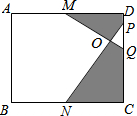 如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=$\frac{1}{4}$DC.若AB=16,BC=20,则图中阴影部分的面积是92.
如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=$\frac{1}{4}$DC.若AB=16,BC=20,则图中阴影部分的面积是92.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了庆祝新年元旦,某商场在门前的空地上用花盆按如图所示的方式搭成正方形.
为了庆祝新年元旦,某商场在门前的空地上用花盆按如图所示的方式搭成正方形.| 正方形的层数n | 1 | 2 | 3 | 4 | … |
| 第n层的花盆数 | 4 | 8 | 12 | 16 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com