
【题目】在□ABCD中,经过A、B、C三点的⊙O与AD相切于点A,经过点C的切线与AD的延长线相交于点P,连接AC.
(1)求证:AB=AC;
(2)若AB=4,⊙O的半径为![]() ,求PD的长.
,求PD的长.

【答案】(1)见解析,(2)![]()
【解析】
(1)连接AO并延长交BC于点E,交⊙O于点F,由切线的性质可得∠FAP=90°,根据平行四边形的性质可得∠AEB=90°,由垂径定理点BE=CE,根据垂直平分线的性质即可得AB=AC;(2)连接FC,OC,设OE=x,则EF=![]() -x,根据AF为直径可得∠ACF=90°,利用勾股定理可得CF的长,利用勾股定理可证明OC2-OE2=CF2-EF2,即可求出x的值,进而可得EC、BC的长,由平行线性质可得∠PAC=∠ACB,由切线长定理可得PA=PC,即可证明∠PAC=∠PCA,由AB=AC可得∠ABC=∠ACB,利用等量代换可得∠ABC=∠PAC,即可证明△PAC∽△ABC,根据相似三角形的性质可求出AP的长,根据PD=AP-AD即可得答案.
-x,根据AF为直径可得∠ACF=90°,利用勾股定理可得CF的长,利用勾股定理可证明OC2-OE2=CF2-EF2,即可求出x的值,进而可得EC、BC的长,由平行线性质可得∠PAC=∠ACB,由切线长定理可得PA=PC,即可证明∠PAC=∠PCA,由AB=AC可得∠ABC=∠ACB,利用等量代换可得∠ABC=∠PAC,即可证明△PAC∽△ABC,根据相似三角形的性质可求出AP的长,根据PD=AP-AD即可得答案.
(1)连接AO并延长交BC于点E,交⊙O于点F.
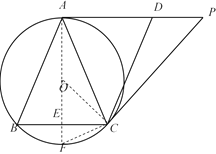
∵AP是⊙O的切线,AF是⊙O的直径,
∴AF⊥AP,
∴∠FAP=90°.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠AEB=∠FAP=90°,
∴AF⊥BC.
∵AF是⊙O的直径,AF⊥BC,
∴BE=CE.
∵AF⊥BC,BE=CE,
∴AB=AC.
(2)连接FC,OC.
设OE=x,则EF=![]() -x.
-x.
∵AF是⊙O的直径,
∴∠ACF=90°.
∵AC=AB=4,AF=2![]() ,
,
∴在Rt△ACF中,∠ACF=90°,
∴CF=![]() =2.
=2.
∵在Rt△OEC中,∠OEC=90°,
∴CE2=OC2-OE2.
∵在Rt△FEC中,∠FEC=90°,
∴CE2=CF2-EF2.
∴OC2-OE2=CF2-EF2.即![]() -x2=22-(
-x2=22-(![]() -x)2.
-x)2.
解得x=![]() .
.
∴EC=![]() =
=![]() .
.
∴BC=2EC=![]() .
.
∵四边形ABCD是平行四边形,
∴AD=BC=![]() .
.
∵AD∥BC,
∴∠PAC=∠ACB.
∵PA,PC是⊙O的切线,
∴PA=PC.
∴∠PAC=∠PCA.
∵AB=AC,
∴∠ABC=∠ACB.
∴∠PAC=∠ABC,∠PCA=∠ACB.
∴△PAC∽△ABC,
∴![]() =
=![]() .
.
∴AP=![]() ·AB=2
·AB=2![]() .
.
∴PD=AP-AD=![]() .
.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】在抗击新型冠状病毒疫情期间,某校学生主动发起为武汉加油捐款活动,为了了解学生捐款金额(单位:元),随机调查了该校的部分学生,根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
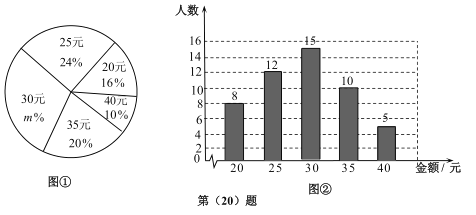
(Ⅰ)本次接受调查的学生人数为_________,图①中m的值为_________;
(Ⅱ)求统计的这组学生捐款数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组学生捐款数据的样本数据,若该校共有1800名学生,估计该校此次捐款总金额为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() (点
(点![]() ,
,![]() 分别与点
分别与点![]() ,
,![]() 对应),
对应),![]() ,
,![]() .
.![]() 固定不动,
固定不动,![]() 运动,并满足点
运动,并满足点![]() 在
在![]() 边从
边从![]() 向
向![]() 移动(点
移动(点![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 始终经过点
始终经过点![]() ,
,![]() 与
与![]() 边交于点
边交于点![]() ,当
,当![]() 是等腰三角形时,
是等腰三角形时,![]() ______.
______.
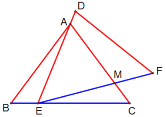
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,随着社会经济的发展,人们的环境保护意识也在逐步增强.某社区设立了“保护环境爱我地球”的宣传牌.已知立杆AB的高度是3m,从地面上某处D点测得宣传牌顶端C点和底端B点的仰角分别是62°和45°.求宣传牌的高度BC的长.(精确到0.1m,参考数据:sin62°=0.83,cos62°=0.47,tan62°=1.88)
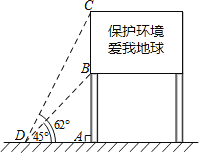
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A、点B在直线![]() 的两侧.
的两侧.
(点A到直线![]() 的距离小于点B到直线
的距离小于点B到直线![]() 的距离).
的距离).
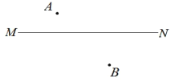
如图, (1)作点B关于直线 (2)以点C为圆心, (3)过点A作 (4)连接 |
|
根据以上作图过程及所作图形,下列四个结论中:
①![]() 是
是![]() 的切线; ②
的切线; ②![]() 平分
平分![]() ;
;
③![]() ; ④
; ④![]() .
.
所有正确结论的序号是___________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点A的坐标为
中,点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,且
,且![]() ,
,![]() .给出如下定义:若平面上存在一点P,使
.给出如下定义:若平面上存在一点P,使![]() 是以线段
是以线段![]() 为斜边的直角三角形,则称点P为点A、点B的“直角点”.
为斜边的直角三角形,则称点P为点A、点B的“直角点”.
(1)已知点A的坐标为![]() .
.
①若点B的坐标为![]() ,在点
,在点![]() 、
、![]() 和
和![]() 中,是点A、点B的“直角点”的是_________;
中,是点A、点B的“直角点”的是_________;
②点B在x轴的正半轴上,且![]() ,当直线
,当直线![]() 上存在点A、点B的“直角点”时,求b的取值范围;
上存在点A、点B的“直角点”时,求b的取值范围;
(2)![]() 的半径为r,点
的半径为r,点![]() 为点
为点![]() 、点
、点![]() 的“直角点”,若使得
的“直角点”,若使得![]() 与
与![]() 有交点,直接写出半径r的取值范围.
有交点,直接写出半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为2的正方形ABCD中,P为AB上的一动点,E为AD中点,PE交CD延长线于Q,过E作EF⊥PQ交BC的延长线于F,则下列结论:①△APE≌△DQE;②PQ=EF;③当P为AB中点时,CF=![]() ;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为1,其中正确的有( )
;④若H为QC的中点,当P从A移动到B时,线段EH扫过的面积为1,其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com