
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于
的图象相交于![]() ,
,![]() 两点.
两点.
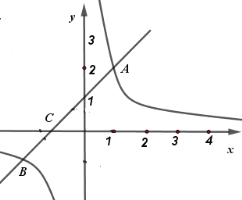
(1)求一次函数和反比例函数的表达式;
(2)直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 轴上的点,若
轴上的点,若![]() 的面积是
的面积是![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)一次函数的表达式为![]() ,反比例函数的表达式为
,反比例函数的表达式为![]() ;(2)(3,0)或(-5,0)
;(2)(3,0)或(-5,0)
【解析】
(1)将点A坐标代入![]() 中求得m,即可得反比例函数的表达式,据此可得点B坐标,再根据A、B两点坐标可得一次函数表达式;
中求得m,即可得反比例函数的表达式,据此可得点B坐标,再根据A、B两点坐标可得一次函数表达式;
(2)设点P(x,0),由题意解得PC的长,进而可得点P坐标.
(1)将点A(1,2)坐标代入![]() 中得:m=1×2=2,
中得:m=1×2=2,
∴反比例函数的表达式为![]() ,
,
将点B(n,-1)代入![]() 中得:
中得:
![]() ,∴n=﹣2,
,∴n=﹣2,
∴B(-2,-1),
将点A(1,2)、B(-2,-1)代入![]() 中得:
中得:
![]() 解得:
解得:![]() ,
,
∴一次函数的表达式为![]() ;
;
(2)设点P(x,0),
∵直线![]() 交
交![]() 轴于点
轴于点![]() ,
,
∴由0=x+1得:x=﹣1,即C(-1,0),
∴PC=∣x+1∣,
∵![]() 的面积是
的面积是![]() ,
,
∴![]()
∴解得:![]() ,
,
∴满足条件的点P坐标为(3,0)或(-5,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
与x轴交于点A(3,0)和点B,与y轴相交于点C(0,3),抛物线的顶点为点D.
(1)求抛物线的表达式及顶点D的坐标;
(2)联结AD、AC、CD,求∠DAC的正切值;
(3)如果点P是原抛物线上的一点,且∠PAB=∠DAC,将原抛物线向右平移m个单位(m>0),使平移后新抛物线经过点P,求平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() 两地相距
两地相距![]() .甲、乙两人都由
.甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]() .
.
(1)根据题意,填写下表:
时间 与 | 0.5 | 1.8 | ______ |
甲与 | 5 | ______ | 20 |
乙与 | 0 | 12 | ______ |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() ,写出
,写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为12,△ABC是等边三角形,点E在正方形ABCD内,对角线AC上有一点P使PE+PD的和最小,这个最小值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
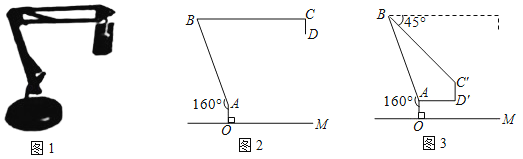
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com