
【题目】将若干枚棋子平均分成三堆(每堆至少2枚),分别放在左边、中间、右边,并按如下顺序进行操作:
第1次:从右边堆中拿出 2枚棋子放入中间一堆;
第2次:从左边一堆中拿出1枚棋子放入中间一堆;
第3次:从中间一堆中拿出几枚棋子放入右边一堆,并使右边一堆的棋子数为最初的2倍.
(1)操作结束后,若右边堆比左边一堆多15枚棋子,问共有_____枚棋子;
(2)通过计算得出:无论最初的棋子数为多少,按上述方法完成操作后,中间一堆总是剩下_____枚棋子.
科目:初中数学 来源: 题型:
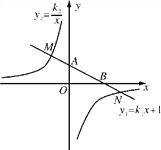
【题目】如图,在平面直角坐标系xOy中,一次函数y1=k1x+1的图象与y轴交于点A,与x轴交于点B,与反比例y2=![]() 象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2.
象分别交于点M,N,已知△AOB的面积为1,点M的纵坐标为2.
(1)求一次函数与反比例函数的解析式;
(2)直接写出y1>y2时,x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
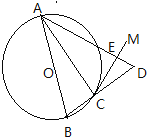
【题目】如图AB是△ABC的外接圆⊙O的直径,过点C作⊙O的切线CM,延长BC到点D,使CD=BC,连接AD交CM于点E,若⊙OD半径为3,AE=5,
(1)求证:CM⊥AD;
(2)求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
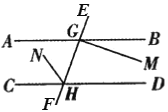
【题目】如图,AB//CD,直线EF与AB、CD分别交于点G、H,GM⊥GE,∠BGM=20°,HN平分∠CHE,则∠NHD的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在∠△ACB和△DCE中,AC=BC,CD=CE,∠ACB=∠DCE=90°,连接AE、BD交于点O,AE与DC交于点M,BD与AC交于点N.试判断AE、BD之间的关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为9,
表示的数为9,![]() 是数轴上一点且
是数轴上一点且![]() .动点
.动点![]() 从点
从点![]() 出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为
出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为![]() (
(![]() )秒.
)秒.
![]()
发现:
(1)写出数轴上点![]() 表示的数 ,点
表示的数 ,点![]() 表示的数 (用含
表示的数 (用含![]() 的代数式表示);
的代数式表示);
探究:
(2)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度沿数轴向左匀速运动, 若点
出发,以每秒2个单位长度的速度沿数轴向左匀速运动, 若点![]() 、
、![]() 同时出发,问
同时出发,问![]() 为何值时点
为何值时点![]() 追上点
追上点![]() ?此时
?此时![]() 点表示的数是多少?
点表示的数是多少?
(3)若![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点,
的三等分点,![]() 是线段
是线段![]() 靠近点
靠近点![]() 的三等分点.点
的三等分点.点![]() 在运动的过程中, 线段
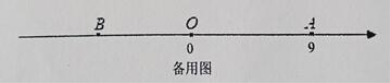
在运动的过程中, 线段![]() 的长度是否发生变化?在备用图中画出图形,并说明理由.
的长度是否发生变化?在备用图中画出图形,并说明理由.

拓展:
(4)若点![]() 是数轴上点,点
是数轴上点,点![]() 表示的数是
表示的数是![]() ,请直接写:
,请直接写:![]() 的最小值是 .
的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
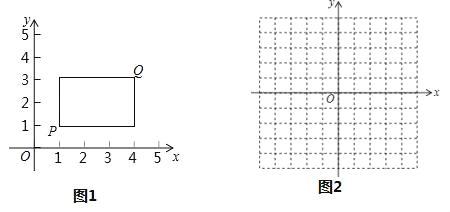
【题目】在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.
(1)已知点A的坐标为(1,0),
①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)正方形RSKT顶点R的坐标为(-1,1),K的坐标为(2,-2),点M的坐标为(m,3),若在正方形RSKT边上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问 有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12 里,13 里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=0.5千米,则该沙田的面积为( ) 平方千米.
A.7.5B.15C.75D.750
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com