
【题目】在每个小正方形的边长为![]() 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距
的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距![]() 的另一个格点的运动称为一次跳马变换.例如,在
的另一个格点的运动称为一次跳马变换.例如,在![]() 的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.现有
的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.现有![]() 的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的N,最少需要跳马变换的次数是_______,现有
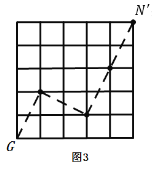
的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的N,最少需要跳马变换的次数是_______,现有![]() 的正方形网格图形(如图3),则从该正方形的顶点
的正方形网格图形(如图3),则从该正方形的顶点![]() 经过跳马变换到达与其相对的
经过跳马变换到达与其相对的![]() ,最少需要跳马变换的次数是_______.
,最少需要跳马变换的次数是_______.

【答案】8 14
【解析】
根据从一个格点移动到与之相距![]() 的另一个格点的运动称为一次跳马变换,计算出按A-C-F的方向连续变换10次后点M的位置,再根据点N的位置进行适当的变换,即可得到变换总次数.
的另一个格点的运动称为一次跳马变换,计算出按A-C-F的方向连续变换10次后点M的位置,再根据点N的位置进行适当的变换,即可得到变换总次数.
如图1,连接AC,CF,则AF=3![]() ,
,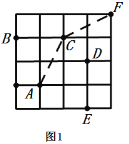
∴两次变换相当于向右移动3格,向上移动3格,
在![]() 的正方形网格图形中:
的正方形网格图形中:
又∵MN=![]() ,
,
∴![]() ,(不是整数)
,(不是整数)
∴按A-C-F的方向连续变换4次后,相当于向右移动了![]() ×3=6格,向上移动了
×3=6格,向上移动了![]() ×3=6格,
×3=6格,
此时M位于如图2所示的4×4的正方形网格的点G处,再按如图所示的方式变换4次即可到达点N处;
故答案为:![]() ;
;
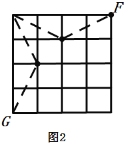
在![]() 的正方形网格图形中:
的正方形网格图形中:
又∵MN=![]() ,
,
∴![]() ,(不是整数)
,(不是整数)
∴按A-C-F的方向连续变换10次后,相当于向右移动了![]() ×3=15格,向上移动了
×3=15格,向上移动了![]() ×3=15格,
×3=15格,
此时![]() 位于如图3所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点
位于如图3所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点![]() 处;
处;
故答案为:![]() ;
;


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,以线段
中,以线段![]() 为边作
为边作![]() ,使得
,使得![]() ,连接
,连接![]() ,再以
,再以![]() 为边作
为边作![]() ,使得
,使得![]() ,
,![]() .
.
(![]() )如图1,连结
)如图1,连结![]() ,求证:
,求证:![]() .
.
(![]() )如图2,
)如图2,![]() 时,将线段
时,将线段![]() 沿着射线
沿着射线![]() 的方向平移,得到线段
的方向平移,得到线段![]() ,连接
,连接![]() ,
,![]() .
.
①若![]() ,依题意补全图2,求线段
,依题意补全图2,求线段![]() 的长.
的长.
②请直接写出线段![]() 的长(用含
的长(用含![]() 的式子表示).
的式子表示).



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,∠C=∠D=90°,AD<BC,BC=CD=6,E是边CD上的一点,恰好使AE=5,并且∠ABE=45°,则CE的长是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() 。
。
(1)请画出![]() 关于
关于![]() 轴对称后得到的
轴对称后得到的![]() ;
;
(2)直接写出点![]() ,点
,点![]() ,点
,点![]() 的坐标;
的坐标;
(3)在![]() 轴上寻找一个点
轴上寻找一个点![]() ,使
,使![]() 的周长最小,并直接写出
的周长最小,并直接写出![]() 的周长的最小值。
的周长的最小值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黑白双雄,纵横江湖;双剑合璧,天下无敌,这是武侠小说中的常见描述,其意思是指两个人合在一起,取长补短,威力无比,在二次根式中也常有这种相辅相成的“对子”,如:![]() ,它们的积中不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解:
,它们的积中不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样解:
 .
.
像这样通过分子、分母同乘一个式子把分母中的根号化去的方法,叫做分母有理化。
解决问题:
(1)![]() 的有理化因式是 ;
的有理化因式是 ;
将![]() 分母有理化得 ;
分母有理化得 ;
(2)已知:![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
港珠澳大桥是中国中央政府支持香港、澳门和珠三角地区城市快速发展的一项重大举措,港珠澳大桥东起香港国际机场附近的香港口岸人工岛,向西横跨伶仃洋海域后连接珠海和澳门,止于珠海洪湾,总长 55 千米,是粤港澳三地首次合作共建的超大型跨海交通工程.某天,甲乙两辆巴士均从香港口岸人工岛出发沿港珠澳大桥开往珠海洪湾,甲巴士平均每小时比乙巴士多行驶 10 千米,其行驶时间是乙巴士行驶时间的![]() .求乘坐甲巴士从香港口岸人工岛出发到珠海洪湾需要多长时间.
.求乘坐甲巴士从香港口岸人工岛出发到珠海洪湾需要多长时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
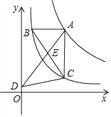
【题目】如图,点A是反比例函数y=![]() 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=
图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=![]() 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在围棋盒中有 x 颗黑色棋子和 y 颗白色棋子,从盒中随机地取出一个棋子,如果它是黑色棋子的概率是![]() ;如果往盒中再放进 10 颗黑色棋子,则取得黑色棋子的概率变为
;如果往盒中再放进 10 颗黑色棋子,则取得黑色棋子的概率变为![]() .求 x 和 y 的值.
.求 x 和 y 的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com