
如图,在▱ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB.
(1)求证:四边形ABCD为菱形;
(2)若AB=12,∠DAB=60°,求四边形ABCD的面积.
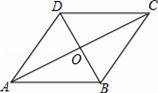

【考点】菱形的判定与性质;平行四边形的性质.
【分析】(1)根据等腰三角形的判定得出AB=BC,根据菱形的判定得出即可;
(2)根据菱形的性质得出AO=OC,BO=OD,AC⊥ND,求出AO、OD,求出AC和BD,根据面积公式求出即可.
【解答】证明:(1)∵∠CAB=∠ACB,
∴AB=BC,
∵四边形ABCD是平行四边形,
∴四边形ABCD为菱形;
(2)∵四边形ABCD为菱形,
∴AC⊥BD,
又∵∠DAB=60°,
∴∠OAB=
 ∠DAB=30°
∠DAB=30°
在Rt△AOB中,
OB=
 AB=
AB=
 ×12=6,
×12=6,
∴OA=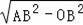
 =
=
 =6
=6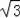
 ,
,
∴BD=20B=12,AC=20A=12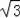
 ,
,
∴S菱形ABCD=
 BD×AC=
BD×AC=
 ×12×12
×12×12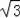
 =72
=72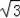
 .
.
【点评】本题考查了勾股定理,菱形的性质和判定的应用,能熟记菱形的性质和判定定理是解此题的关键.


科目:初中数学 来源: 题型:
如图,已知抛物线y=ax2+bx+3交x轴于A、B两点(A在B左边),交y轴于C点,且OC=3OA,对称轴x=1交抛物线于D点.
(1)求抛物线解析式;
(2)求证:△BCD为直角三角形;
(3)在x轴上方的抛物线上,是否存在点M,过M作MN⊥x轴于N点,使△BMN与△BCD相似?若存在,请求出M的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4400000000人,这个数用科学记数法表示为( )
A.44×108 B.4.4×109 C.4.4×108 D.4.4×1010
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com