
【题目】计算
(1) (4a3b-6a2b2+12ab3)÷2ab
(2) a3·a4·a+(a2)4+(-2a4)2
(3) ![]()
(4)![]()
(5)![]()
【答案】(1)2a2-3ab+6b2;(2)6a8;(3)3x2-4xy-5y2;(4)x2-11x+6;(5)![]()
【解析】
(1)根据多项式除以单项式法则计算可得;
(2)根据先根据同底数幂乘法、幂的乘方、积的乘方法则计算;再合并同类项即可;
(3)根据先利用平方差公式和完全平方公式计算,再进行加减运算可得.
(4)根据单项式、多项式乘以多项式的运算法则计算可得;
(5)原式先利用零指数幂、负整数指数幂等法则计算乘方运算,再有理数加减运算即可得到结果;
解:(1) (4a3b-6a2b2+12ab3)÷2ab,
=2a2-3ab+6b2;
(2) a3·a4·a+(a2)4+(-2a4)2,
=![]() ,
,
=![]() ,
,
=![]() ;
;
(3) ![]() ,
,
=![]() ,
,
=![]() ,
,
=![]() ;
;
(4)![]() ,
,
=![]() ,
,
=![]() ,
,
=![]()
(5)![]()
=1-![]() +9-4
+9-4
=![]() .
.


科目:初中数学 来源: 题型:
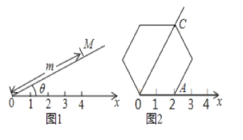
【题目】阅读理如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”。应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
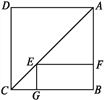
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是计算机中的一种益智小游戏“扫雷”的画面,在一个![]() 的小方格的正方形 雷区中,随机埋藏着
的小方格的正方形 雷区中,随机埋藏着![]() 颗地雷,每个小方格内最多只能埋藏
颗地雷,每个小方格内最多只能埋藏![]() 颗地雷。小红在游戏开始时首先随机的点击一个方格,该方格中出现了数字“
颗地雷。小红在游戏开始时首先随机的点击一个方格,该方格中出现了数字“![]() ”,其意义表示该格的外围区域(图中阴影部分,记为
”,其意义表示该格的外围区域(图中阴影部分,记为![]() 区域)有
区域)有![]() 颗地雷;接着小红又点击了左上角第一个方格,出现了数字“
颗地雷;接着小红又点击了左上角第一个方格,出现了数字“![]() ”,其外围区域(图中阴影)记为
”,其外围区域(图中阴影)记为![]() 区域;
区域;![]() 区域与
区域与![]() 区域以及出现数字“
区域以及出现数字“![]() ”和“
”和“![]() ”两格以外的部分记为
”两格以外的部分记为![]() 区域。请分别计算出
区域。请分别计算出![]() 区、
区、![]() 区、
区、![]() 区点中地雷的概率,那么她应点击
区点中地雷的概率,那么她应点击![]() 、
、![]() 、
、![]() 中的哪个区域?
中的哪个区域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
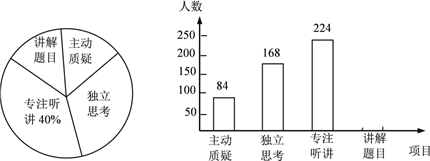
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的角平分线.
(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 在直角坐标系中,
在直角坐标系中,

(1)请写出![]() 顶点在第一象限内的坐标;
顶点在第一象限内的坐标;
(2)若把![]() 向上平移
向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度得到
个单位长度得到![]() ,画出平移后的图形;
,画出平移后的图形;
(3)求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为

A. ![]() B. 5C. 3D.
B. 5C. 3D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com