
分析 分式的化简,要熟悉混合运算的顺序,分子、分母能因式分解的先因式分解;除法要统一为乘法运算,注意化简后,将x=$\frac{1}{2}$代入化简后的式子求出即可.
解答 解:$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$÷$\frac{x+1}{x-1}$×$\frac{1-x}{1+x}$,
=$\frac{(x+1)(x-1)}{(x-1)^{2}}$×$\frac{x-1}{x+1}$×$\frac{1-x}{x+1}$,
=$\frac{x+1}{x-1}$×$\frac{x-1}{x+1}$×$\frac{1-x}{x+1}$,
=$\frac{1-x}{x+1}$;
当x=$\frac{1}{2}$时,原式=$\frac{1-\frac{1}{2}}{\frac{1}{2}+1}$=$\frac{\frac{1}{2}}{\frac{3}{2}}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题主要考查了分式混合运算,要注意分子、分母能因式分解的先因式分解;除法要统一为乘法运算是解题关键.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
 如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC
如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC查看答案和解析>>
科目:初中数学 来源: 题型:填空题
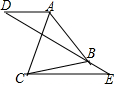 如图,直线DE过等边△ABC的顶点B,连接AD、CE,AD∥CE,∠E=30°,若BE:AD=1:$\sqrt{3}$,CE=4$\sqrt{3}$时,则BC=2$\sqrt{7}$.
如图,直线DE过等边△ABC的顶点B,连接AD、CE,AD∥CE,∠E=30°,若BE:AD=1:$\sqrt{3}$,CE=4$\sqrt{3}$时,则BC=2$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 随着互联网的发展,同学们的学习习惯也有了改变,一些在做题遇到困难时,喜欢上网查找答案,针对这个问题,某校调查了部分学生对这种做法的意见(分为:赞成、无所谓、反对),并将调查结果绘制成图1和图2两个不完整的统计图,请根据图中提供的信息,解答下列问题:
随着互联网的发展,同学们的学习习惯也有了改变,一些在做题遇到困难时,喜欢上网查找答案,针对这个问题,某校调查了部分学生对这种做法的意见(分为:赞成、无所谓、反对),并将调查结果绘制成图1和图2两个不完整的统计图,请根据图中提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50% | B. | 40% | C. | 30% | D. | 20% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
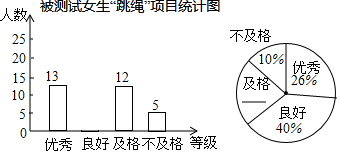
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com