
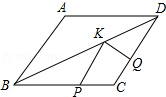
 如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )
如图,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为( )| A. | 2 | B. | $\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
分析 根据轴对称确定最短路线问题,作点P关于BD的对称点P′,连接P′Q与BD的交点即为所求的点K,然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值,然后求解即可.
解答 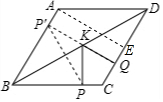 解:如图,菱形ABCD中,∵AB=2,∠A=120°,
解:如图,菱形ABCD中,∵AB=2,∠A=120°,
∴AD=2,∠ADC=60°,
过A作AE⊥CD于E,
则AE=P′Q,
∵AE=AD•cos60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴点P′到CD的距离为$\sqrt{3}$,
∴PK+QK的最小值为$\sqrt{3}$.
故选B.
点评 本题考查了菱形的性质,轴对称确定最短路线问题,熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 )数,如图,一层二叉树的结点总数为1,二层二叉树的点总数为3,三层二叉树的结点总数为7,…照此规律,你认为八层二叉树的结点总数为( )
)数,如图,一层二叉树的结点总数为1,二层二叉树的点总数为3,三层二叉树的结点总数为7,…照此规律,你认为八层二叉树的结点总数为( )
| A. | 127 | B. | 168 | C. | 255 | D. | 512 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
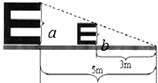 根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )
根据测试距离为5m的标准视力表制作一个测试距离为3m的视力表,如果标准视力表中“E”的长a是3.6cm,那么制作出的视力表中相应“E”的长b是( )| A. | 1.44cm | B. | 2.16cm | C. | 2.4cm | D. | 3.6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
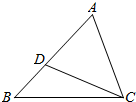 如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.
如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com