
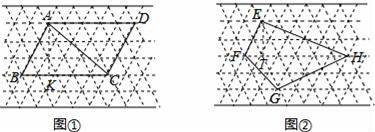
如图中的虚线网格我们称为正三角形网格,它的每一个小三角形都是边长为1个单位长度的正三角形,这样的三角形称为单位正三角形.
(1)图①中,已知四边形ABCD是平行四边形,求△ABC的面积和对角线AC的长;
(2)图②中,求四边形EFGH的面积.


【考点】平行四边形的性质;三角形的面积;等边三角形的性质;勾股定理.
【分析】(1)首先过点A作AK⊥BC于K,由每一个小三角形都是边长为1个单位长度的正三角形,可求得该小正三角形的高为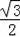
 ,则可求得△ABC的面积,然后由勾股定理求得对角线AC的长;
,则可求得△ABC的面积,然后由勾股定理求得对角线AC的长;
(2)首先过点E作ET⊥FH于T,即可得四边形EFGH的面积为:2S△EFH=2×
 ×ET×FH.
×ET×FH.
【解答】解:(1)由图①,过点A作AK⊥BC于K,
∵每一个小三角形都是边长为1个单位长度的正三角形.
∴该小正三角形的高为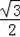
 ,
,
则:S△ABC=
 ×AK×CB=
×AK×CB=
 ×3×
×3×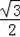
 ×CB=
×CB=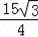
 ;
;
∵AK=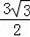
 ,BK=
,BK=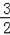
 ,
,
∴KC=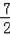
 ,
,
故由勾股定理可求得:AC=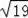
 .
.
(2)由图②,过点E作ET⊥FH于T,
又由题意可知:四边形EFGH的面积为:2S△EFH=2×
 ×ET×FH=ET×FH=2×
×ET×FH=ET×FH=2×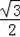
 ×6=6
×6=6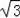
 .
.



科目:初中数学 来源: 题型:
用配方法解方程x2+8x-7=0,则配方正确的是( )
A.(x+4)2=23 B.(x﹣4)2=23 C.(x﹣8)2=49  D.(x+8)2=64
D.(x+8)2=64
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知在矩形ABCD中,AD=10,CD=5,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,当B、E、F三点共线时,两点同时停止运动,此时BF⊥CE.设点E移动的时间为t(秒).
(1)求当t为何值时,两点同时停止运动;
(2)求当t为何值时,EC是∠BED的平分线;
(3)设四边形BCFE的面积为S,求S与t之间的函数关系式,并写出t的取值范围;
(4)求当t为何值时,△EFC是等腰三角形.(直接写出答案)


查看答案和解析>>
科目:初中数学 来源: 题型:
.在△ABC中,D是BC边的中点,E、F分别在AD及其延长线上,CE∥BF,连接BE、CF.
(1)求证:△BDF≌△CDE;
(2)若DE=
 BC,试判断四边形BFCE是怎样的四边形,并证明你的结论.
BC,试判断四边形BFCE是怎样的四边形,并证明你的结论.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com