
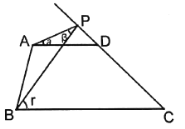
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ACΘΫBCΘΫ2Θ§ΓœCΘΫ90ΓψΘ§ΫΪ“ΜΩιΒ»―ϋ»ΐΫ«ΑεΒΡ÷±Ϋ«ΕΞΒψΖ≈‘Ύ–±±ΏABΒΡ÷–ΒψP¥ΠΘ§ΫΪ»ΐΫ«Αε»ΤΒψP–ΐΉΣΘ§»ΐΫ«ΑεΒΡΝΫ÷±Ϋ«±ΏΖ÷±πΫΜ…δœΏACΓΔCB”ΎDΓΔEΝΫΒψΘ°»γΆΦΔΌΓΔΔΎΓΔΔέ «–ΐΉΣ»ΐΫ«ΑεΒΟΒΫΒΡΆΦ–Έ÷–ΒΡ3÷÷«ιΩωΘ§―–ΨΩΘΚ
Θ®1Θ©»ΐΫ«Αε»ΤΒψP–ΐΉΣΘ§Ιέ≤λœΏΕΈPD”κPE÷°Φδ”– ≤Ο¥ ΐΝΩΙΊœΒΘΩΫαΚœΆΦΔΎΥΒΟςάμ”…Θ°
Θ®2Θ©»ΐΫ«Αε»ΤΒψP–ΐΉΣΘ§ΓςPCE «ΖώΡή≥…ΈΣΒ»―ϋ»ΐΫ«–ΈΘΩ»τΡήΘ§÷Η≥ωΥυ”–«ιΩωΘ®÷±Ϋ”–¥¥πΑΗΘ©Θ°
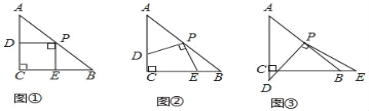
ΓΨ¥πΑΗΓΩΘ®1Θ©PD=PE,÷ΛΟςΦϊΫβΈωΘΜΘ®2Θ©ΓςPCEΡή≥…ΈΣΒ»―ϋ»ΐΫ«–ΈΘ§÷ΛΟςΦϊΫβΈω
ΓΨΫβΈωΓΩ
Θ®1Θ©PD=PEΘ§Ά®Ιΐ÷ΛΓςDPCΓ’ΓςEPBΘ§Ω…ΒΟΫα¬έ
Θ®2Θ©Ζ÷»ΐ÷÷«ιΩωΧ÷¬έΔΌΒ±PCΘΫPEΘΫ![]() ±ΘΜΔΎΒ±PCΘΫCEΘΫ
±ΘΜΔΎΒ±PCΘΫCEΘΫ![]() ±ΘΜΔέΒ±PEΘΫEC ±Θ§Ω…«σΫβΘ°
±ΘΜΔέΒ±PEΘΫEC ±Θ§Ω…«σΫβΘ°
Ϋβ:Θ®1Θ©PD=PEΘ§άμ”…»γœ¬ΘΚ
Β±D‘ΎAC…œ ±Θ§Ν§Ϋ”PCΘ§

“ρΈΣΓςABC «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§P «ABΒΡ÷–ΒψΘ§
ΓύCP=PBΘ§CPΓΆABΘ§ΓœACP=![]() ΓœACB=45ΓψΘ°
ΓœACB=45ΓψΘ°
ΓύΓœACP=ΓœB=45ΓψΘ°
”÷ΓΏΓœDPC+ΓœCPE=ΓœBPE+ΓœCPEΘ§
ΓύΓœDPC=ΓœBPEΘ°
ΓύΓςPCDΓ’ΓςPBEΘ°
ΓύPD=PEΘΜ
Β±D‘ΎAC…œ ±Θ§Ν§Ϋ”PCΘ§

“ρΈΣΓςABC «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§P «ABΒΡ÷–ΒψΘ§
ΓύCP=PBΘ§CPΓΆABΘ§ΓœACP=![]() ΓœACB=45ΓψΘ°
ΓœACB=45ΓψΘ°
ΓύΓœACP=ΓœCBP=45ΓψΘ°
ΓύΓœPCD=ΓœPBE=135ΓψΘ°
”÷ΓΏΓœDPC+ΓœDPB=ΓœDPB+ΓœBPEΘ§
ΓύΓœDPC=ΓœBPEΘ°
ΓύΓςPCDΓ’ΓςPBEΘ°
ΓύPD=PE
Ήέ…œΥυ ωΘΚPD=PEΘΜ
Θ®2Θ©ΓςPBE «Β»―ϋ»ΐΫ«–ΈΘ§άμ”…»γœ¬ΘΚ
ΓΏACΘΫBCΘΫ2Θ§ΓœCΘΫ90Γψ
ΓύABΘΫ2![]()
ΓύAPΘΫBPΘΫCPΘΫ![]()
ΓςPCE «Β»―ϋ»ΐΫ«–Έ
Β±PCΘΫPEΘΫ![]() ±Θ§Φ¥BΘ§E÷ΊΚœΘ§BEΘΫ0
±Θ§Φ¥BΘ§E÷ΊΚœΘ§BEΘΫ0
Β±PCΘΫCEΘΫ![]() ±Θ§«“E‘ΎœΏΕΈBC…œΘ§‘ρBEΘΫ2©¹
±Θ§«“E‘ΎœΏΕΈBC…œΘ§‘ρBEΘΫ2©¹![]()
Β±PCΘΫCEΘΫ![]() ±Θ§«“E‘ΎœΏΕΈBCΒΡ―”≥ΛœΏ…œΘ§‘ρBEΘΫ2+
±Θ§«“E‘ΎœΏΕΈBCΒΡ―”≥ΛœΏ…œΘ§‘ρBEΘΫ2+![]()
Β±PEΘΫECΘ§«“ΓœPCBΘΫ45Γψ
ΓύΓœPECΘΫ90Γψ
ΓύECΘΫ1
ΓύBEΘΫ1



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ–Γ”±ΚΆ–ΓΝΝ…œ…Ϋ”ΈΆφΘ§–Γ”±≥ΥΉχά¬≥ΒΘ§–ΓΝΝ≤Ϋ––Θ§ΝΫ»Υœύ‘Φ‘Ύ…ΫΕΞΒΡά¬≥Β÷’ΒψΜαΚœ.“―÷Σ–ΓΝΝ––ΉΏΒΫά¬≥Β÷’ΒψΒΡ¬Ζ≥Χ «ά¬≥ΒΒΫ…ΫΕΞΒΡœΏ¬Ζ≥ΛΒΡ2±ΕΘ§–Γ”±‘Ύ–ΓΝΝ≥ωΖΔΚσ50Ζ÷≤≈≥Υ…œά¬≥ΒΘ§ά¬≥ΒΒΡΤΫΨυΥΌΕ»ΈΣ180ΟΉ/Ζ÷Θ§…η–ΓΝΝ≥ωΖΔxΖ÷Κσ––ΉΏΒΡ¬Ζ≥ΧΈΣyΟΉΘ°ΆΦ÷–ΒΡ’έœΏ±μ Ψ–ΓΝΝ‘Ύ’ϊΗω––ΉΏΙΐ≥Χ÷–yΥφxΒΡ±δΜ·ΙΊœΒ.
Θ®1)–ΓΝΝ––ΉΏΒΡΉή¬Ζ≥Χ «_________ΟΉΘ§ΥϊΆΨ÷––ίœΔΝΥ___________Ζ÷ΘΜ
Θ®2Θ©Ζ÷±π«σ≥ω–ΓΝΝ‘Ύ–ίœΔ«ΑΚΆ–ίœΔΚσΥυΉΏΒΡ¬Ζ≥ΧΕΈ…œΒΡ≤Ϋ––ΥΌΕ»ΘΜ
Θ®3Θ©Β±–Γ”±ΒΫ¥οά¬≥Β÷’Βψ ±Θ§–ΓΝΝάκά¬≥Β÷’ΒψΒΡ¬Ζ≥Χ «Εύ…ΌΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
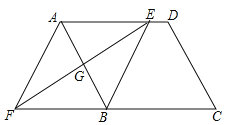
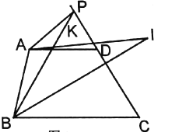
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫ––ΥΡ±Ώ–ΈABCD÷–Θ§±ΏABΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜAD”ΎΒψEΘ§ΫΜCBΒΡ―”≥ΛœΏ”ΎΒψFΘ§Ν§Ϋ”AFΘ§BEΘ°
Θ®1Θ©«σ÷ΛΘΚΓςAGEΓ’ΓςBGFΘΜ
Θ®2Θ© ‘≈–ΕœΥΡ±Ώ–ΈAFBEΒΡ–ΈΉ¥Θ§≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
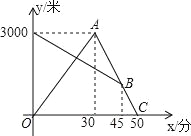
ΓΨΧβΡΩΓΩΡ≥Χλ‘γ≥ΩΘ§’≈«Ω¥”Φ“≈ή≤Ϋ»ΞΧε”ΐΕΆΝΕΘ§Ά§ ±¬η¬η¥”Χε”ΐ≥Γ≥ΩΝΖΫα χΜΊΦ“Θ§ΆΨ÷–ΝΫ»Υœύ”ωΘ§’≈«Ω≈ήΒΫΧε”ΐ≥ΓΚσΖΔœ÷“Σœ¬”ξΘ§ΝΔΦ¥Α¥‘≠¬ΖΖΒΜΊΘ§”ωΒΫ¬η¬ηΚσΝΫ»Υ“ΜΤπΜΊΒΫΦ“Θ®’≈«ΩΚΆ¬η¬η Φ÷’‘ΎΆ§“ΜΧθ± ÷±ΒΡΙΪ¬Ζ…œ––ΉΏΘ©Θ°»γΆΦ «ΝΫ»ΥάκΦ“ΒΡΨύάκyΘ®ΟΉΘ©”κ’≈«Ω≥ωΖΔΒΡ ±ΦδxΘ®Ζ÷Θ©÷°ΦδΒΡΚ· ΐΆΦœσΘ§ΗυΨίΆΦœσ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©«σ’≈«ΩΖΒΜΊ ±ΒΡΥΌΕ»ΘΜ
Θ®2Θ©¬η¬η±»Α¥‘≠ΥΌΖΒΜΊΧα«ΑΕύ…ΌΖ÷÷”ΒΫΦ“ΘΩ
Θ®3Θ©«κ÷±Ϋ”–¥≥ω’≈«Ω”κ¬η¬ηΚΈ ±œύΨύ1000ΟΉΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΥΡ±Ώ–Έ![]() Θ§
Θ§![]() Θ§Βψ
Θ§Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œ‘ΥΕ·(Βψ
…œ‘ΥΕ·(Βψ![]() ΚΆΒψ
ΚΆΒψ![]() Θ§
Θ§![]() ≤Μ÷ΊΚœΘ§Βψ
≤Μ÷ΊΚœΘ§Βψ![]() Θ§
Θ§![]() Θ§
Θ§![]() ≤Μ‘ΎΆ§“ΜΧθ÷±œΏ…œ)Θ§»τΦ«
≤Μ‘ΎΆ§“ΜΧθ÷±œΏ…œ)Θ§»τΦ«![]() Θ§
Θ§![]() Θ§
Θ§![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
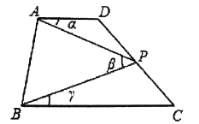
ΆΦ1 ΆΦ2 ΆΦ3
(1)»γΆΦ1Θ§Β±Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ‘ΥΕ· ±Θ§–¥≥ω
…œ‘ΥΕ· ±Θ§–¥≥ω![]() Θ§
Θ§![]() Θ§
Θ§![]() ÷°ΦδΒΡΙΊœΒΘ§≤ΔΥΒ≥ωάμ”…ΘΜ
÷°ΦδΒΡΙΊœΒΘ§≤ΔΥΒ≥ωάμ”…ΘΜ
(2)»γΆΦ2Θ§»γΙϊΒψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() ΒΡ―”≥ΛœΏ…œ‘ΥΕ·Θ§ΧΫΨΩ
ΒΡ―”≥ΛœΏ…œ‘ΥΕ·Θ§ΧΫΨΩ![]() Θ§
Θ§![]() Θ§
Θ§![]() ÷°ΦδΒΡΙΊœΒΘ§≤ΔΥΒΟςάμ”….
÷°ΦδΒΡΙΊœΒΘ§≤ΔΥΒΟςάμ”….
(3)»γΆΦ3Θ§![]() ΤΫΖ÷
ΤΫΖ÷![]() Θ§
Θ§![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§«“
Θ§«“![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§«σ
Θ§«σ![]() ΒΡΕ» ΐ.
ΒΡΕ» ΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
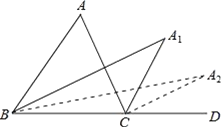
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœA=mΓψΘ§ΓœABCΚΆΓœACDΒΡΤΫΖ÷œΏΫΜ”ΎΒψA1Θ§ΒΟΓœA1ΘΜΓœA1BCΚΆΓœA1CDΒΡΤΫΖ÷œΏΫΜ”ΎΒψA2Θ§ΒΟΓœA2ΘΜΓ≠ΓœA2015BCΚΆΓœA20l5CDΒΡΤΫΖ÷œΏΫΜ”ΎΒψA2016Θ§‘ρΓœA2016=__Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®![]() Ζ÷Θ©»γΆΦΘ§Ιή÷–Ζ≈÷ΟΉ≈»ΐΗυΆ§―υΒΡ…ΰΉ”
Ζ÷Θ©»γΆΦΘ§Ιή÷–Ζ≈÷ΟΉ≈»ΐΗυΆ§―υΒΡ…ΰΉ”![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() Θ°
Θ°
Θ®![]() Θ©–ΓΟς¥”
Θ©–ΓΟς¥”![]() ’β»ΐΗυ…ΰΉ”÷–ΥφΜζ―Γ“ΜΗυΘ§«ΓΚΟ―Γ÷–…ΰΉ”
’β»ΐΗυ…ΰΉ”÷–ΥφΜζ―Γ“ΜΗυΘ§«ΓΚΟ―Γ÷–…ΰΉ”![]() ΒΡΗ≈¬ «__________Θ°
ΒΡΗ≈¬ «__________Θ°
Θ®![]() Θ©–ΓΟςœ»¥”ΉσΕΥ
Θ©–ΓΟςœ»¥”ΉσΕΥ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() »ΐΗω…ΰΆΖ÷–ΥφΜζ―ΓΝΫΗω¥ρ“ΜΗωΫαΘ§‘Ό¥””“ΕΥ
»ΐΗω…ΰΆΖ÷–ΥφΜζ―ΓΝΫΗω¥ρ“ΜΗωΫαΘ§‘Ό¥””“ΕΥ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() »ΐΗω…ΰΆΖ÷–ΥφΜζ―ΓΝΫΗω¥ρ“ΜΗωΫαΘ§«σ’β»ΐΗυ…ΰΉ”ΡήΝ§Ϋα≥…“ΜΗυ≥Λ…ΰΒΡΗ≈¬ Θ°
»ΐΗω…ΰΆΖ÷–ΥφΜζ―ΓΝΫΗω¥ρ“ΜΗωΫαΘ§«σ’β»ΐΗυ…ΰΉ”ΡήΝ§Ϋα≥…“ΜΗυ≥Λ…ΰΒΡΗ≈¬ Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
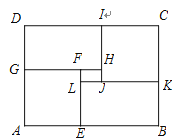
ΓΨΧβΡΩΓΩ‘ΎΨΊ–ΈABCD÷–Θ§AB=8Θ§BC=6Θ§ΫΪΨΊ–ΈΑ¥ΆΦ ΨΖΫ ΫΫχ––Ζ÷ΗνΘ§Τδ÷–’ΐΖΫ–ΈAEFG”κ’ΐΖΫ–ΈJKCI»ΪΒ»Θ§ΨΊ–ΈGHID”κΨΊ–ΈEBKL»ΪΒ»Θ°
Θ®1Θ©Β±ΨΊ–ΈLJHFΒΡΟφΜΐΈΣ![]() ±Θ§«σAGΒΡ≥ΛΘΜ
±Θ§«σAGΒΡ≥ΛΘΜ
Θ®2Θ©Β±AGΈΣΚΈ÷Β ±Θ§ΨΊ–ΈLJHFΒΡΟφΜΐΉν¥σΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΦ”«Ω―ß…ζΩΈΆβ‘ΡΕΝΘ§ΩΣάΪ ”“ΑΘ§Ρ≥–ΘΩΣ’ΙΝΥΓΑ ιœψ–Θ‘ΑΘ§Υ–ΕΝΨ≠ΒδΓ±ΜνΕ·Θ§―ßœΑΥφΜζ≥ι≤ιΝΥ≤ΩΖ÷―ß…ζΘ§Ε‘ΥϊΟ«ΟΩΧλΒΡΩΈΆβ‘ΡΕΝ ±ΦδΫχ––Βς≤ιΘ§≤ΔΫΪΒς≤ιΆ≥ΦΤΒΡΫαΙϊΖ÷ΈΣΥΡάύΘΚΟΩΧλΥ–ΕΝ ±ΦδtΓή20Ζ÷÷”ΒΡ―ß…ζΦ«ΈΣAάύΘ§20Ζ÷÷”ΘΦtΓή40Ζ÷÷”Φ«ΈΣBάύΘ§40Ζ÷÷”ΘΦtΓή60Ζ÷÷”Φ«ΈΣCάύΘ§tΘΨ60Ζ÷÷”Φ«ΈΣDάύΘ§ ’Φ·ΒΡ ΐΨίΜφ÷Τ»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ°«κΗυΨίΆΦ÷–ΧαΙ©ΒΡ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ

Θ®1Θ©’β¥ΈΙ≤≥ι»ΓΝΥΓΓ ΓΓΟϊ―ß…ζΫχ––Βς≤ιΆ≥ΦΤΘ§…»–ΈΆ≥ΦΤΆΦ÷–DάύΥυΕ‘”ΠΒΡ…»–Έ‘≤–ΡΫ«¥σ–ΓΈΣΓΓ ΓΓΘΜ
Θ®2Θ©ΫΪΧθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
Θ®3Θ©»γΙϊΗΟ–ΘΙ≤”–2000Οϊ―ß…ζΘ§«κΡψΙάΦΤΗΟ–ΘCάύ―ß…ζ‘Φ”–Εύ…Ό»ΥΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com