
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2019年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示:
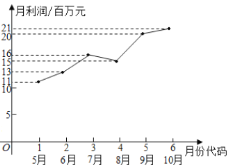
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2020年4月份的利润;
的线性回归方程,并预测该公司2020年4月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有A,B两种型号的新型材料可供选择,按规定每种新型材料最多可使用4个月,但新材料的不稳定性会导致材料的使用寿命不同,现对A,B两种型号的新型材料对应的产品各100件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:

经甲公司测算平均每件新型材料每月可以带来6万元收人入,不考虑除采购成本之外的其他成本,A型号材料每件的采购成本为10万元,B型号材料每件的采购成本为12万元.假设每件新型材料的使用寿命都是整月数,且以频率作为每件新型材料使用寿命的概率,如果你是甲公司的负责人,以每件新型材料产生利润的平均值为决策依据,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() ,其中
,其中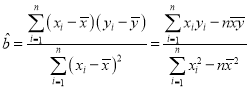 .
.
【答案】(1)线性回归方程为![]() ,利润为33百万元;(2)应该采购A型新材料.
,利润为33百万元;(2)应该采购A型新材料.
【解析】
(1)根据题设的折线图中的统计数据,求得其平均数,以及回归系数![]() 和
和![]() ,求得回归直线的方程,代入
,求得回归直线的方程,代入![]() 时,即可作出预测;
时,即可作出预测;
(2)由频率估计概率,求得每件A,B型新材料可产生的利润的平均值,即可得到结论.
(1)由题意,根据题设的折线图可知,统计数据![]() 共有6组,
共有6组,
即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
计算可得![]() ,
,![]() ,
,
所以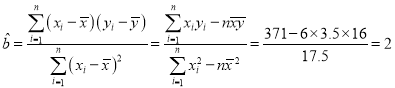 ,
,
![]() ,
,
所以月度利润![]() 与月份代码
与月份代码![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
当![]() 时,可得
时,可得![]() .
.
故预计甲公司2020年4月份的利润为33百万元.
(2)由频率估计概率,每件A型新材料可使用1个月,2个月,3个月和4个月的概率,
分别为0.2,0.35,0.35和0.1,
所以每件A型新材料可产生的利润的平均值为
![]() (万元).
(万元).
由频率估计概率,每件B型新材料可使用1个月,2个月,3个月和4个月的概率,
分别为0.15,0.2,0.4和0.25,
所以每件B型新材料可产生的利润的平均值为
![]() (万元).
(万元).
因为![]() ,所以应该采购A型新材料.
,所以应该采购A型新材料.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】某人经营淡水池塘养草鱼,根据过去![]() 期的养殖档案,该池塘的养殖重量
期的养殖档案,该池塘的养殖重量![]() (百斤)都在
(百斤)都在![]() 百斤以上,其中不足
百斤以上,其中不足![]() 百斤的有
百斤的有![]() 期,不低于
期,不低于![]() 百斤且不超过
百斤且不超过![]() 百斤的有
百斤的有![]() 期,超过
期,超过![]() 百斤的有
百斤的有![]() 期.根据统计,该池塘的草鱼重量的增加量
期.根据统计,该池塘的草鱼重量的增加量![]() (百斤)与使用某种饵料的质量
(百斤)与使用某种饵料的质量![]() (百斤)之间的关系如图所示.
(百斤)之间的关系如图所示.
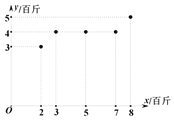
(1)根据数据可知![]() 与
与![]() 具有线性相关关系,请建立
具有线性相关关系,请建立![]() 关于
关于![]() 的回归方程
的回归方程![]() ;如果此人设想使用某种饵料
;如果此人设想使用某种饵料![]() 百斤时,草鱼重量的增加量须多于
百斤时,草鱼重量的增加量须多于![]() 百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.
百斤,请根据回归方程计算,确定此方案是否可行?并说明理由.
(2)养鱼的池塘对水质含氧量与新鲜度要求较高,某商家为该养殖户提供收费服务,即提供不超过![]() 台增氧冲水机,每期养殖使用的冲水机运行台数与鱼塘的鱼重量
台增氧冲水机,每期养殖使用的冲水机运行台数与鱼塘的鱼重量![]() 有如下关系:
有如下关系:
鱼的重量(单位:百斤) |
|
|
|
冲水机只需运行台数 |
|
|
|
若某台增氧冲水机运行,则商家每期可获利![]() 千元;若某台冲水机未运行,则商家每期亏损
千元;若某台冲水机未运行,则商家每期亏损![]() 千元.视频率为概率,商家欲使每期冲水机总利润的均值达到最大,应提供几台增氧冲水机?
千元.视频率为概率,商家欲使每期冲水机总利润的均值达到最大,应提供几台增氧冲水机?
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为
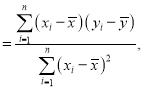
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣sinx,记f(x)的导函数为f'(x).
(1)若h(x)=ax![]() f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
f'(x)是(0,+∞)上的单调递增函数,求实数a的取值范围;
(2)若x∈(0,2π),试判断函数f(x)的极值点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是平面![]() 的斜线段,A为斜足,点C满足
的斜线段,A为斜足,点C满足![]() ,且在平面
,且在平面![]() 内运动,则有以下几个命题:
内运动,则有以下几个命题:

①当![]() 时,点C的轨迹是抛物线;
时,点C的轨迹是抛物线;
②当![]() 时,点C的轨迹是一条直线;
时,点C的轨迹是一条直线;
③当![]() 时,点C的轨迹是圆;
时,点C的轨迹是圆;
④当![]() 时,点C的轨迹是椭圆;
时,点C的轨迹是椭圆;
⑤当![]() 时,点C的轨迹是双曲线.
时,点C的轨迹是双曲线.
其中正确的命题是__________.(将所有正确的命题序号填到横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
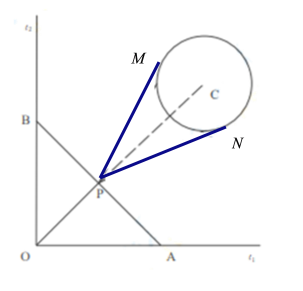
【题目】如图,在一旅游区内原有两条互相垂直且相交于点O的道路l1,l2,一自然景观的边界近似为圆形,其半径约为1千米,景观的中心C到l1,l2的距离相等,点C到点O的距离约为10千米.现拟新建四条游览道路方便游客参观,具体方案:在线段OC上取一点P,新建一条道路OP,并过点P新建两条与圆C相切的道路PM,PN(M,N为切点),同时过点P新建一条与OP垂直的道路AB(A,B分别在l1,l2上).为促进沿途旅游经济,新建道路长度之和越大越好,求新建道路长度之和的最大值.(所有道路宽度忽略不计)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题12分)
A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后观察疗效。若在一个试验组中,服用A有效的小白鼠的只数比服用B有效的多,就称该试验组为甲类组。设每只小白鼠服用A有效的概率为![]() ,服用B有效的概率为
,服用B有效的概率为![]() 。
。
(Ⅰ)求一个试验组为甲类组的概率;
(Ⅱ) 观察3个试验组,用![]() 表示这3个试验组中甲类组的个数,求
表示这3个试验组中甲类组的个数,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com