
【题目】已知函数![]() .
.
(1)若函数![]() 在其定义域内单调递增,求实数
在其定义域内单调递增,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使得函数
,使得函数![]() 的图象与
的图象与![]() 轴相切?若存在,求满足条件的
轴相切?若存在,求满足条件的![]() 的取值范围,请说明理由.
的取值范围,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)根据导数和函数的单调性的关系,分离参数,即可求出![]() 的取值范围;
的取值范围;
(2)函数![]() 的图象与
的图象与![]() 轴相切,且存在
轴相切,且存在![]() 的极值等于0,根据导数和函数的极值的关系即可求出答案.
的极值等于0,根据导数和函数的极值的关系即可求出答案.
(1)![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,在
,在![]() 上恒成立,
上恒成立,
即![]() ,
,
易知![]() 在
在![]() 上为增函数,
上为增函数,
∴![]() ,
,
∴![]() ;
;
(2)函数![]() ,
,
设![]() ,
,
∴![]()
![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ,
,
①当![]() 时,即
时,即![]() 时,当
时,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() ,解得
,解得![]() (舍去),
(舍去),
②当![]() 时,
时,![]() ,即极值点为
,即极值点为![]() 或
或![]() ,
,
∵函数![]() 的图象与
的图象与![]() 轴相切,
轴相切,
∴![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
当![]() 时,可得
时,可得![]() ,
,
设![]() ,则
,则![]() ,
,
则![]() ,
,
即![]() ,
,
设![]() ,
,
∴![]() ,
,
再令![]()
∴![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
∴![]() ,
,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∵![]() ,
,
∴存在![]() ,使得
,使得![]() ,
,
即![]() ,即
,即![]() ,
,
综上所述存在实数一个实数![]() ,得使得函数
,得使得函数![]() 的图象与
的图象与![]() 轴相切.
轴相切.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】科学家为研究对某病毒有效的疫苗,通过小鼠进行毒性和药效预实验.为了比较注射A,B两种疫苗后产生的抗体情况,选200只小鼠做实验,将这200只小鼠随机分成两组,每组100只,其中一组注射疫苗A,另一组注射疫苗B.下表1和表2分别是注射疫苗A和疫苗B后的实验结果.
表1:注射疫苗A后产生抗体参数的频率分布表
抗体参数 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2:注射疫苗B后产生抗体参数的频率分布表
抗体参数 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
(1)完成下面频率分布直方图,并比较注射两种疫苗后抗体参数的中位数大小;
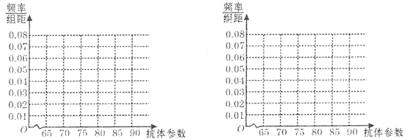
(2)完成下面2×2列联表,并回答能否有99.9%的把握认为“注射疫苗A后的抗体参数与注射疫苗B后的抗体参数有差异”.
表3:
抗体参数小于75 | 抗体参数不小于75 | 合计 | |
注射疫苗A | a= | b= | |
注射疫苗B | c= | d= | |
合计 | n= |
附: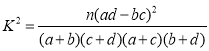
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十八大以来,脱贫工作取得巨大成效,全国农村贫困人口大幅减少.如图的统计图反映了2012﹣2019年我国农村贫困人口和农村贫困发生率的变化情况(注:贫困发生率=贫困人数(人)÷统计人数(人)×100%).根据统计图提供的信息,下列推断不正确的是( )
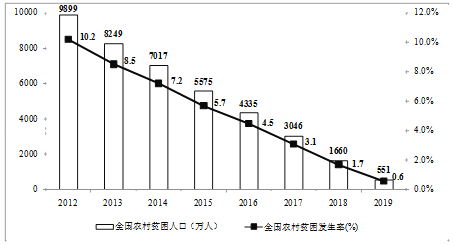
A.2012﹣2019年,全国农村贫困人口逐年递减
B.2013﹣2019年,全国农村贫困发生率较上年下降最多的是2013年
C.2012﹣2019年,全国农村贫困人口数累计减少9348万
D.2019年,全国各省份的农村贫困发生率都不可能超过0.6%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】BMI指数(身体质量指数,英文为BodyMassIndex,简称BMI)是衡量人体胖瘦程度的一个标准,BMI=体重(kg)/身高(m)的平方.根据中国肥胖问题工作组标准,当BMI≥28时为肥胖.某地区随机调查了1200名35岁以上成人的身体健康状况,其中有200名高血压患者,被调查者的频率分布直方图如下:
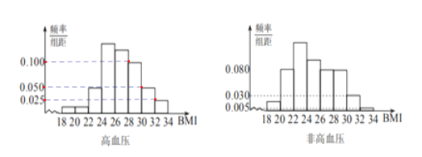
(1)求被调查者中肥胖人群的BMI平均值![]() ;
;
(2)填写下面列联表,并判断是否有99.9%的把握认为35岁以上成人患高血压与肥胖有关.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合计 | |
高血压 | |||
非高血压 | |||
合计 |
附: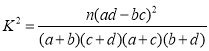 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,已知可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病.而今年出现在湖北武汉的新型冠状病毒(nCoV)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等,在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.医院为筛查冠状病毒,需要检验血液是否为阳性,现有![]() 份血液样本,有以下两种检验方式:
份血液样本,有以下两种检验方式:
方式一:逐份检验,则需要检验![]() 次.
次.
方式二:混合检验,将其中![]() (
(![]() 且
且![]() )份血液样本分别取样混合在一起检验.
)份血液样本分别取样混合在一起检验.
若检验结果为阴性,这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() .假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)现有![]() 份血液样本,其中只有
份血液样本,其中只有![]() 份样本为阳性,若采用逐份检验方式,求恰好经
份样本为阳性,若采用逐份检验方式,求恰好经![]() 次检验就能把阳性样本全部检验出来的概率.
次检验就能把阳性样本全部检验出来的概率.
(2)现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次为
,采用混合检验方式,样本需要检验的总次为![]() .
.
(i)若![]() ,试求
,试求![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ;
;
(ii)若![]() ,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求
,且采用混合检验方式可以使得样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求![]() 的最大值.
的最大值.
参考数据:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com