
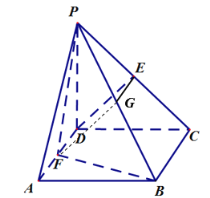
【题目】如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E、F分别是PC、AD中点,
(1)求证:DE//平面PFB;
(2)求PB与面PCD所成角的正切值。

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)取PB的中点G,连接EG,FG,通过证明四边形FGED是平行四边形,得ED//GF,进而可以得到DE//面PFB;
(2)先由条件求出∠BPC就是PB与面PCD所成的角,再通过求三角形边长即可得到结论
(1)取PB的中点G,连接EG,FG,如图,
![]() E,G分别是PC,PB的中点,
E,G分别是PC,PB的中点,
![]() FG//BC且FG=
FG//BC且FG=![]() BC,又DF//BC且DF=
BC,又DF//BC且DF=![]() BC
BC
![]() FG//DF且FG=DF,
FG//DF且FG=DF,
![]() 四边形FGED是平行四边形,
四边形FGED是平行四边形,
则DE//GF,又DE![]() 面PFB,GF
面PFB,GF![]() 面PFB,
面PFB,
![]() DE//面PFB
DE//面PFB
(2)由已知得:PD⊥面ABCD
∴PD⊥BC
∵ABCD是正方形
∴BC⊥CD
又PD∩CD=D
∴BC⊥面PCD
∴PB在面PCD内的射影是PC
∴∠BPC就是PB与面PCD所成的角.
设PD=DC=a,则PC=![]()
∴在△PBC中,∠PCB=90°,PC=![]() ,BC=a
,BC=a
∴tan∠BPC=![]()
∴PC与面PCD所成角的正切值为![]()


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只红铃虫的产卵数y和温度x有关,现收集了7组观测数据如下表:
温度x/℃ | 21 | 23 | 25 | 27 | 29 | 32 | 35 |
产卵个数y/个 | 7 | 11 | 21 | 24 | 66 | 115 | 325 |
(I)根据散点图判断,![]() 与
与![]() 哪一个适宜作为产卵数
哪一个适宜作为产卵数![]() 关于温度
关于温度![]() 的回归方程类型(给出判断即可,不必说明理由);
的回归方程类型(给出判断即可,不必说明理由);
(II)根据(I)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(Ⅲ)红铃虫是棉区危害较重的害虫,可从农业、物理和化学三个方面进行防治,其中农业方面防治有3种方法,物理方面防治有1种方法,化学方面防治3种方法,现从7种方法中选3种方法进行综合防治(即3种方法不能全部来自同一方面,至少来自两个方面),X表示在综合防治中农业方面的防治方法的种数,求X的分布列及数学期望E(X).
附:可能用到的公式及数据表中(表中![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() ,
,![]() =
=![]()
![]() )
)
|
|
|
|
|
|
|
27.430 | 3.612 | 81.290 | 147.700 | 2763.764 | 705.592 | 40.180 |
对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
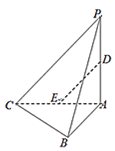
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() .设
.设![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点.
中点.
(1)求证:![]()
![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)试问在线段![]() 上是否存在点
上是否存在点![]() ,使得过三点
,使得过三点![]() ,
,![]() ,
,![]() 的平面内的任一条直线都与平面
的平面内的任一条直线都与平面![]() 平行?若存在,指出点
平行?若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为:
的方程为:![]() .
.
(1)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)圆![]() 上有一动点
上有一动点![]() ,
,![]() ,若向量
,若向量![]() ,求动点
,求动点![]() 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理财公司有两种理财产品A和B,这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品A
投资结果 | 获利40% | 不赔不赚 | 亏损20% |
概率 |
|
|
|
产品B
投资结果 | 获利20% | 不赔不赚 | 亏损10% |
概率 | p |
| q |
注:p>0,q>0
(1)已知甲、乙两人分别选择了产品A和产品B投资,如果一年后他们中至少有一人获利的概率大于![]() ,求实数p的取值范围;
,求实数p的取值范围;
(2)若丙要将家中闲置的10万元人民币进行投资,以一年后投资收益的期望值为决策依据,则选用哪种产品投资较理想?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若函数f(x)=ax2+bx+3a+b是偶函数,定义域为[a-1,2a],则a=________,b=________;
(2)已知函数f(x)=ax2+2x是奇函数,则实数a=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() 这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.
这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.

在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,已知 ,
,已知 ,![]() .
.
(1)求![]() ;
;
(2)如图,![]() 为边
为边![]() 上一点,
上一点,![]() ,求
,求![]() 的面积
的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com