
【题目】已知![]() 为定义在R上的奇函数,当
为定义在R上的奇函数,当![]() 时,
时,![]() 为二次函数,且满足
为二次函数,且满足![]() ,
,![]() 在
在![]() 上的两个零点为
上的两个零点为![]() 和
和![]() .
.
(1)求函数![]() 在R上的解析式;
在R上的解析式;
(2)作出![]() 的图象,并根据图象讨论关于
的图象,并根据图象讨论关于![]() 的方程
的方程![]()
![]() 根的个数.
根的个数.
【答案】(1)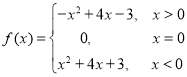 ;(2)当
;(2)当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;当
个根;当![]() 或
或![]() 时,方程有
时,方程有![]() 个根; 当
个根; 当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;当
个根;当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;
个根;
【解析】
试题分析:(1)当![]() 时,根据
时,根据![]() 在
在![]() 上的两个零点为
上的两个零点为![]() 和
和![]() ,设函数为两根式即
,设函数为两根式即![]() ,
,![]() ,所以解得
,所以解得![]() ,当
,当![]() 时,
时,![]() ,∵
,∵![]() 为
为![]() 上的奇函数,∴
上的奇函数,∴![]() ,求得解析式为
,求得解析式为![]() ,因为奇函数
,因为奇函数![]() ,可得函数解析式;(2)关于
,可得函数解析式;(2)关于![]() 的方程
的方程![]()
![]() 根的个数,即函数
根的个数,即函数![]() 与
与![]() 交点的个数,作出
交点的个数,作出![]() 的图象可得
的图象可得
试题分析:(1)由题意,当![]() 时,设
时,设![]() ,
,
![]() ,∴
,∴![]() ,∴
,∴![]()
(注:设![]() 一样给分)
一样给分)
当![]() 时,
时,![]() ,∵
,∵![]() 为
为![]() 上的奇函数,∴
上的奇函数,∴![]() ,
,
∴![]()
即![]() 时,
时,![]()
当![]() 时,由
时,由![]() 得:
得:![]()
所以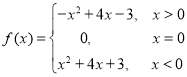 .
.
(2)作出![]() 的图象(如图所示)
的图象(如图所示)

(注:![]() 的点或两空心点不标注扣1分,
的点或两空心点不标注扣1分,
不要重复扣分)
由![]() 得:
得:![]() ,在图中作
,在图中作![]() ,
,
根据交点讨论方程的根:
当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;
个根;
当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;
个根;
当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;
个根;
当![]() 或
或![]() 时,方程有
时,方程有![]() 个根;
个根;
当![]() 时,方程有
时,方程有![]() 个根.
个根.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,AB=BC=1,BB1=2,∠BCC1=60°。
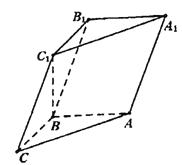
(Ⅰ)求证:C1B⊥平面ABC;
(Ⅱ)设![]() (0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
(0≤λ≤1),且平面AB1E与BB1E所成的锐二面角的大小为30°,试求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形ABCD和正方形ABEF的边长都是1,并且平面ABCD⊥平面ABEF,点M在AC上移动,点N在BF上移动.若|CM|=|BN|=a(0<a<![]() ).
).
(1)求MN的长度;
(2)当a为何值时,MN的长度最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次国际学术会议上,来自四个国家的五位代表被安排坐在一张圆桌,为了使他们能够自由交谈,事先了解到的情况如下:
甲是中国人,还会说英语.
乙是法国人,还会说日语.
丙是英国人,还会说法语.
丁是日本人,还会说汉语.
戊是法国人,还会说德语.
则这五位代表的座位顺序应为( )
A. 甲丙丁戊乙 B. 甲丁丙乙戊
C. 甲乙丙丁戊 D. 甲丙戊乙丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率.
附:线性回归方程![]() 中系数计算公式
中系数计算公式 ,
, ![]() ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com