
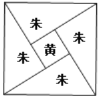
����Ŀ������ʱ�������ѧ����ˬ��ע�������㾭���и����˹��ɶ����ľ���֤��.��������ˬ����ͼ��ע�ģ���ͼ��һ���Թ�����֮��Ϊ�ߵ������Σ��������Ϊ��ʵ��ͼ�а����ĸ�ȫ�ȵĹ����μ�һ��С�����Σ��ֱ�Ϳ�ɺ죨�죩ɫ����ɫ���������Ϊ��ʵ��ʵ������![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��ʵ
��ʵ![]() ��ʵ
��ʵ![]() ��ʵ�����ù�
��ʵ�����ù�![]() ��
��![]() ��
��![]() ���蹴���й��ɱ�Ϊ
���蹴���й��ɱ�Ϊ![]() ��������ͼ���������
��������ͼ���������![]() ��ͼ������С���Բ��ƣ��������ڻ�ɫͼ���ڵ�ͼ��������ԼΪ�� �����ο�����
��ͼ������С���Բ��ƣ��������ڻ�ɫͼ���ڵ�ͼ��������ԼΪ�� �����ο�����![]() ��
��![]() ��
��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����![]() ,
,![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ,
,![]() ,ֱ��
,ֱ��![]() ,
,![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ,�����ǵ�б��֮��Ϊ-2,���
,�����ǵ�б��֮��Ϊ-2,���![]() �Ĺ켣������
�Ĺ켣������![]() .
.
��1��������![]() �ķ���;
�ķ���;
��2����ֱ֪��![]() ������
������![]() �ཻ�ڲ�ͬ����
�ཻ�ڲ�ͬ����![]() ��
��![]() ���������������ϵĵ㣩,������
���������������ϵĵ㣩,������![]() ��
��![]() ��������ύ�ڵ�
��������ύ�ڵ�![]() ,��
,��![]() ,����Ϊ
,����Ϊ![]() ��
��![]() ,��֤��ֱ��
,��֤��ֱ��![]() �������.
�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4 ����ϵ���������
��֪����![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ������
������![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������������
Ϊ������������![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������.
������.
����������![]() ��
��![]() �����㣬����ʵ��
�����㣬����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
����������![]() �IJ���������
�IJ���������![]() ��������
��������![]() ��
��![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
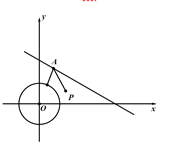
����Ŀ���ƴ�ʫ��������ʫ���ŴӾ��С���ͷ����˵:�����յ�ɽ����𣬻ƻ�����������.��ʫ��������һ����Ȥ����ѧ�����������������������������ڹ������֮���ɽ����ij���������ȵ��ӱ������ٻص���Ӫ�������߲���ʹ��·�����?����ͼ��ʾ��ֱ������ϵ![]() �У����Ӫ����ƽ������Ϊ
�У����Ӫ����ƽ������Ϊ![]() ���Ӱ�������ֱ�߷���Ϊ
���Ӱ�������ֱ�߷���Ϊ![]() .�ٶ������ӵ�
.�ٶ������ӵ�![]() ��������ֻҪ�����Ӫ�������ص���Ӫ��������ѡ�����·��Ϊ_____________.
��������ֻҪ�����Ӫ�������ص���Ӫ��������ѡ�����·��Ϊ_____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ھ���ABCD�У�AB��3![]() ��BC��3���ضԽ���BD����BCD����ʹ��C�Ƶ�C��㣬��C�����ƽ��ABD�ϵ���ӰOǡ��AB�ϣ�
��BC��3���ضԽ���BD����BCD����ʹ��C�Ƶ�C��㣬��C�����ƽ��ABD�ϵ���ӰOǡ��AB�ϣ�
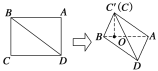
(1)��֤��BC���ƽ��AC��D��
(2)���A��ƽ��BC��D�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪С��ÿ���������ʮ���ĸ��ʶ�Ϊ40%���ֲ������ģ��ķ�������С���������ǡ����������ʮ���ĸ��ʣ����ɼ���������0��9֮��ȡ����ֵ���������ָ��2��4��6��8��ʾ����ʮ����0��1��3��5��7��9��ʾδ����ʮ��������ÿ���������Ϊһ�飬������������Ľ���������ģ�����������20���������
321 421 292 925 274 632 800 478 598 663 531 297 396
021 506 318 230 113 507 965
�ݴ˹��ƣ�С���������ǡ����������ʮ���ĸ���Ϊ����
A. 0.25B. 0.30C. 0.35D. 0.40
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ��ֱ��
��ֱ��![]() ��
��
��1����֤��ֱ��![]() ������㣻
������㣻
��2���ж�ֱ��![]() ��Բ
��Բ![]() �صõ��ҳ���ʱ�����ʱ���?����صõ��ҳ����ʱ����
�صõ��ҳ���ʱ�����ʱ���?����صõ��ҳ����ʱ����![]() ��ֵ�Լ���̳���.
��ֵ�Լ���̳���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ߵĶ���![]() ������ԭ�㣬������
������ԭ�㣬������![]() �Ḻ�����ϣ�����
�Ḻ�����ϣ�����![]() ��ֱ��
��ֱ��![]() �뒁�����ཻ��
�뒁�����ཻ��![]() ���㣬������
���㣬������![]() .
.
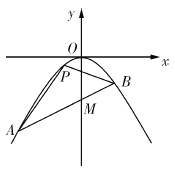
��1����ֱ��![]() �͒����ߵķ��̣�
�͒����ߵķ��̣�
��2������������һ����![]() �ӵ�
�ӵ�![]() �˶�����
�˶�����![]() ʱ����
ʱ����![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]() ��ԭ������б��Ϊ
��ԭ������б��Ϊ![]() .������ԭ��
.������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ��������Ϊ���Ὠ������ϵ������
��������Ϊ���Ὠ������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() .��ƽ��ֱ������ϵ
.��ƽ��ֱ������ϵ![]() �У�����
������![]() ������
������![]() ����ֱ��
����ֱ��![]() �Գ�.
�Գ�.
����������![]() �ļ����귽�̣�
�ļ����귽�̣�
������ֱ��![]() ��ԭ������б��Ϊ
��ԭ������б��Ϊ![]() ����ֱ��
����ֱ��![]() ������
������![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬ֱ��
���㣬ֱ��![]() ������
������![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬��
���㣬��![]() �仯ʱ����
�仯ʱ����![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com