
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时,![]() ②函数
②函数![]() 有3个零点
有3个零点
③![]() 的解集为
的解集为![]() ④
④![]() ,都有
,都有![]()
其中正确命题的个数是( )
A. 4B. 3C. 2D. 1
【答案】A
【解析】
对于①:根据奇函数的性质即可求解;
对于②:先求出当![]() 时,函数的零点,利用奇函数的性质,就可以求出当
时,函数的零点,利用奇函数的性质,就可以求出当![]() 时,函数的零点,由于函数
时,函数的零点,由于函数![]() 是定义在
是定义在![]() 上的奇函数,所以有
上的奇函数,所以有![]() 。
。
对于③:分类讨论,当![]() 时,求出
时,求出![]() 的解集;当
的解集;当![]() 时,求出
时,求出![]() 的解集。
的解集。
对于④:利用导数,求出函数![]() 的值域,就可以判断是否正确。
的值域,就可以判断是否正确。
对于①:当![]() 时,有
时,有![]() ,由奇函数定义可知:
,由奇函数定义可知:![]() ,所以
,所以
![]() 本命题正确;
本命题正确;
对于②:当![]() 时,
时,![]() ,解得
,解得![]() ,即
,即![]() ,根据奇函数的性质可知
,根据奇函数的性质可知![]() ,又因为定义域是
,又因为定义域是![]() ,所以
,所以![]() ,因此函数
,因此函数![]() 有3个零点,本命题正确;
有3个零点,本命题正确;
对于③:当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() ;
;
当![]() 时,通过①的分析,可知
时,通过①的分析,可知![]() ,当
,当![]() 时,即
时,即![]() ,解得
,解得![]() ,
,![]() ,本命题正确;
,本命题正确;
对于④:当![]() 时,
时,![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,函数单调递增;当
,函数单调递增;当![]()
![]() ,函数单调递减,
,函数单调递减,
![]()
![]() 的极大值为
的极大值为![]() ,
,
当![]() 时,
时,![]() ,根据③可知,当
,根据③可知,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() ,由于
,由于![]() 是奇函数
是奇函数![]() 时,
时,![]() ,
,
而![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]() 恒成立,本命题正确。
恒成立,本命题正确。
综上所述,有4个命题是正确的,因此本题选A。


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. “![]() ”是“
”是“![]() ”成立的充分不必要条件
”成立的充分不必要条件
B. 命题![]() ,则
,则![]()
C. 为了了解800名学生对学校某项教改试验的意见,用系统抽样的方法从中抽取一个容量为40的样本,则分组的组距为40
D. 已知回归直线的斜率的估计值为1.23,样本点的中心为![]() ,则回归直线方程为
,则回归直线方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有标号为![]() 的
的![]() 张标签,随机的选取两张标签.
张标签,随机的选取两张标签.
(1)若标签的选取是无放回的,求两张标签上的数字为相邻整数的概率;
(2)若标签的选取是有放回的,求两张标签上的数字至少有一个为5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代第一部数学专著,全书总结了战国、秦、汉时期的数学成就。“更相减损术”便出自其中,原文记载如下:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。”其核心思想编译成如示框图,若输入的![]() ,
,![]() 分别为45,63,则输出的
分别为45,63,则输出的![]() 为( )
为( )
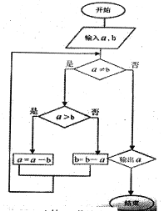
A. 2B. 3C. 5D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆锥的高,
是圆锥的高,![]() 是圆锥底面的直径,
是圆锥底面的直径,![]() 是底面圆周上一点,
是底面圆周上一点,![]() 是
是![]() 的中点,平面
的中点,平面![]() 和平面
和平面![]() 将圆锥截去部分后的几何体如图所示.
将圆锥截去部分后的几何体如图所示.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,AB∥CD,AB![]() ,E为PC中点.
,E为PC中点.
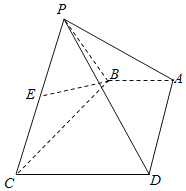
(Ⅰ)证明:BE∥平面PAD;
(Ⅱ)若AB⊥平面PBC,△PBC是边长为2的正三角形,求点E到平面PAD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以平面直角坐标系的原点为极点,
),以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 被圆截得的弦长为
被圆截得的弦长为![]() 时,求
时,求![]() 的值.
的值.
(2)直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),若
为参数),若![]() ,垂足为
,垂足为![]() ,求
,求![]() 点的极坐标.
点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的个数是_________.
(1)命题“若![]() ,则方程
,则方程![]() 有实数根”的逆否命题为“若方程
有实数根”的逆否命题为“若方程![]() 无实数根,则
无实数根,则![]() ”.
”.
(2)命题“![]() ,
,![]() ”的否定“
”的否定“![]() ,
,![]() ”.
”.
(3)若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题.
均为假命题.
(4)“![]() ”是“直线
”是“直线![]() :
:![]() 与直线
与直线![]() :
:![]() 平行”的充要条件.
平行”的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某市高三教学质量检测中,全市共有5000名学生参加了本次考试,其中示范性高中参加考试学生人数为2000人,非示范性高中参加考试学生人数为3000人.现从所有参加考试的学生中随机抽取100人,作检测成绩数据分析.

(1)设计合理的抽样方案(说明抽样方法和样本构成即可);
(2)依据100人的数学成绩绘制了如图所示的频率分布直方图,据此估计本次检测全市学生数学成绩的平均分;
(3)如果规定成绩不低于130分为特别优秀,现已知语文特别优秀占样本人数的![]() ,语文、数学两科都特别优秀的共有3人,依据以上样本数据,完成列联表,并分析是否有
,语文、数学两科都特别优秀的共有3人,依据以上样本数据,完成列联表,并分析是否有![]() 的把握认为语文特别优秀的同学,数学也特别优秀.
的把握认为语文特别优秀的同学,数学也特别优秀.
语文特别优秀 | 语文不特别优秀 | 合计 | |
数学特别优秀 | |||
数学不特别优秀 | |||
合计 |
参考公式:![]()
参考数据:
| 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com