
【题目】已知函数![]() ,函数
,函数![]() 是区间
是区间![]() 上的减函数.
上的减函数.
(1)求![]() 的最大值;
的最大值;
(2)若![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(3)讨论关于![]() 的方程
的方程![]() 的根的个数.
的根的个数.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() ,即
,即![]() 时,方程无解;当
时,方程无解;当![]() ,即
,即![]() 时,方程有一个解;当
时,方程有一个解;当![]() ,即
,即![]() 时,方程有两个解.
时,方程有两个解.
【解析】试题分析:(1)由题意由于![]() ,所以函数
,所以函数![]() ,又因为该函数在区间
,又因为该函数在区间![]() 上的减函数,所以可以得到
上的减函数,所以可以得到![]() 的范围;(2)由于
的范围;(2)由于![]() 在
在![]() 上恒成立
上恒成立![]() ,解出即可;(3)利用方程与函数的关系可以构造成两函数图形的交点个数加以分析求解.
,解出即可;(3)利用方程与函数的关系可以构造成两函数图形的交点个数加以分析求解.
试题解析:(1)∵![]() ,∴
,∴![]() ,
,
又∵![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() 在
在![]() 恒成立,
恒成立,
∴![]() ,∴故
,∴故![]() 的最大值为-1;
的最大值为-1;
(2)∵![]() ,
,
∴只需![]() 在
在![]() 上恒成立,
上恒成立,
既![]() ,
,
令![]() ,
,
则需则![]() ,
,
又∵![]() 恒成立,∴
恒成立,∴![]() ;
;
(3)由于![]() ,令
,令![]() ,
,
∵![]() ,∴当
,∴当![]() 时,
时, ![]() ,即
,即![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,即
,即![]() 单调递减,∴
单调递减,∴![]() ,
,
又∵![]() ,
,
∴当![]() ,即
,即![]() 时,方程无解;
时,方程无解;
当![]() ,即
,即![]() 时,方程有一个解;
时,方程有一个解;
当![]() ,即
,即![]() 时,方程有两个解.
时,方程有两个解.


科目:高中数学 来源: 题型:
【题目】从装有![]() 个红球和
个红球和![]() 个黒球的口袋内任取
个黒球的口袋内任取![]() 个球,则互为对立事件是( )
个球,则互为对立事件是( )
A. 至少有一个黒球与都是黒球B. 至少有一个黒球与都是红球
C. 至少有一个黒球与至少有![]() 个红球D. 恰有
个红球D. 恰有![]() 个黒球与恰有
个黒球与恰有![]() 个黒球
个黒球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某养殖的水产品在临近收获时,工人随机从水中捕捞![]() 只,其质量分别在
只,其质量分别在![]()
![]() (单位:克),经统计分布直方图如图所示.
(单位:克),经统计分布直方图如图所示.

(1)求这组数据的众数;
(2)现按分层抽样从质量为![]() 的水产品种随机抽取
的水产品种随机抽取![]() 只,在从这
只,在从这![]() 只中随机抽取
只中随机抽取![]() 只,求这
只,求这![]() 只水产品恰有
只水产品恰有![]() 只在
只在![]() 内的概率;
内的概率;
(3)某经销商来收购水产品时,该养殖场现还有水产品共计约![]() 只要出售,经销商提出如下两种方案:
只要出售,经销商提出如下两种方案:
方案A:所有水产品以![]() 元/只收购;
元/只收购;
方案B:对于质量低于![]() 克的水产品以
克的水产品以![]() 元/只收购,不低于
元/只收购,不低于![]() 克的以
克的以![]() 元/只收购,
元/只收购,
通过计算确定养殖场选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,右焦点为圆
,右焦点为圆![]() 的圆心,且圆
的圆心,且圆![]() 截
截![]() 轴所得弦长为4.
轴所得弦长为4.
(1)求椭圆![]() 与圆
与圆![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() ,
,![]() 都只有一个公共点,记直线
都只有一个公共点,记直线![]() 与圆
与圆![]() 的公共点为
的公共点为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如右下表所示(![]() (吨)为买进蔬菜的质量,
(吨)为买进蔬菜的质量,![]() (天)为销售天数):
(天)为销售天数):
(Ⅰ) 根据右表提供的数据在网格中绘制散点图,并判断![]() 与
与![]() 是否线性相关,若线性相关,用最小二乘法求出
是否线性相关,若线性相关,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()

| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅱ)根据(Ⅰ)中的计算结果,若该蔬菜商店准备一次性买进蔬菜25吨,则预计需要销售多少天.
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.

(1)用五点法画出这个函数在一个周期内的图像;(必须列表)
(2)求它的振幅、周期、初相、对称轴方程;
(3)说明此函数图象可由![]() 在
在![]() 上的图象经过怎样的变换得到.
上的图象经过怎样的变换得到.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l的参数方程为 (其中t为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=6cosθ.
(其中t为参数).现以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=6cosθ.
(Ⅰ)写出直线l普通方程和曲线C的直角坐标方程;
(Ⅱ)过点M(-1,0)且与直线l平行的直线l1交C于A,B两点,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
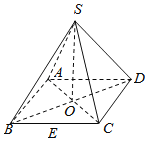
【题目】如图,四棱锥![]() 中,底面是边长为
中,底面是边长为![]() 的正方形ABCD,AC与BD的交点为O,
的正方形ABCD,AC与BD的交点为O,![]() 平面ABCD且
平面ABCD且![]() ,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持
,E是边BC的中点,动点P在四棱锥表面上运动,并且总保持![]() ,则动点P的轨迹的周长为( )
,则动点P的轨迹的周长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 且
且![]() .圆C与直线
.圆C与直线![]() 相切于点A,且点A的纵坐标为
相切于点A,且点A的纵坐标为![]() ,圆心C在直线
,圆心C在直线![]() 上.
上.
(1)求直线![]() 之间的距离;
之间的距离;
(2)求圆C的标准方程;
(3)若直线![]() 经过点
经过点![]() 且与圆C交于
且与圆C交于![]() 两点,当△CPQ的面积最大时,求直线
两点,当△CPQ的面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com