
【题目】已知数列![]() 中,
中, ![]() ,数列
,数列![]() 满足
满足![]() .
.
(1)求证:数列![]() 是等差数列,写出
是等差数列,写出![]() 的通项公式;
的通项公式;
(2)求数列![]() 的通项公式及数列
的通项公式及数列![]() 中的最大项与最小项.
中的最大项与最小项.
【答案】(1)详见解析;(2)![]() ,
, ![]() .
.
【解析】试题分析:(Ⅰ)首先通过已知条件![]() 化简变形,凑出
化简变形,凑出![]() 这种形式,凑出
这种形式,凑出![]() 常数,
常数,
就可以证明数列![]() 是等差数列,并利用等差数列的通项公式求出
是等差数列,并利用等差数列的通项公式求出![]() 通项公式;(Ⅱ)因为
通项公式;(Ⅱ)因为![]() 与
与![]() 有关,所以利用
有关,所以利用![]() 的通项公式求出数列
的通项公式求出数列![]() 的通项公式,把通项公式看成函数,利用函数图像求最大值和最小值.
的通项公式,把通项公式看成函数,利用函数图像求最大值和最小值.
试题解析:(Ⅰ)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴数列
,∴数列![]() 是以1为公差的等差数列. 4分
是以1为公差的等差数列. 4分
∵![]() ,∴
,∴![]() ,又∵
,又∵![]() ,
, ![]() ,
,
∴![]() 是以
是以![]() 为首项,
为首项, ![]() 为公差的等差中项.
为公差的等差中项.
∴![]() ,
, ![]() . 7分
. 7分
(Ⅱ)∵![]() ,
, 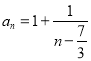 ,
, ![]() .
.
∴作函数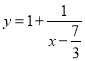 的图像如图所示:
的图像如图所示:
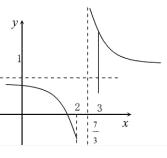
∴由图知,在数列![]() 中,最大项为
中,最大项为![]() ,最小项为
,最小项为![]() . 13分
. 13分
另解: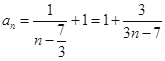 ,当
,当![]() 时,数列
时,数列![]() 是递减数列,且
是递减数列,且![]() .
.
列举![]() ;
;![]() ;
;![]() .所以在数列
.所以在数列![]() 中,最大项为
中,最大项为![]() ,最小项为
,最小项为![]() .
.


科目:高中数学 来源: 题型:
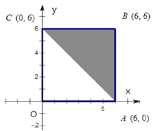
【题目】如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界)。
(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程![]() ,其左焦点、上顶点和左顶点分别为
,其左焦点、上顶点和左顶点分别为![]() ,
, ![]() ,
, ![]() ,坐标原点为
,坐标原点为![]() ,且线段
,且线段![]() ,
, ![]() ,
, ![]() 的长度成等差数列.
的长度成等差数列.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若过点![]() 的一条直线
的一条直线![]() 交椭圆于点
交椭圆于点![]() ,
, ![]() ,交
,交![]() 轴于点
轴于点![]() ,使得线段
,使得线段![]() 被点
被点![]() ,
, ![]() 三等分,求直线
三等分,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处. 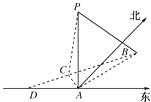
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是平行四边行,
是平行四边行, ![]() 平面
平面![]() ,
, ![]() //
// ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)证明: ![]() //平面
//平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(4)求二面角![]() 的平面角的正切值.
的平面角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com