
【题目】已知等差数列![]() 的公差d>0,则下列四个命题:
的公差d>0,则下列四个命题:
①数列![]() 是递增数列; ②数列
是递增数列; ②数列![]() 是递增数列;
是递增数列;
③数列![]() 是递增数列; ④数列
是递增数列; ④数列![]() 是递增数列.
是递增数列.
其中正确命题的个数为( )
A.1B.2C.3D.4
【答案】B
【解析】
根据等差数列的通项公式和前![]() 项和公式,结合数列的通项公式的函数性质进行求解即可.
项和公式,结合数列的通项公式的函数性质进行求解即可.
①:因为数列![]() 是等差数列,
是等差数列,
所以![]() ,
,
因此可以把![]() 看成关于
看成关于![]() 的一次函数,
的一次函数,
而![]() ,所以数列
,所以数列![]() 是递增数列,因此本命题是真命题;
是递增数列,因此本命题是真命题;
②:因为数列![]() 是等差数列,
是等差数列,
所以![]() ,
,
因此可以把![]() 看成关于
看成关于![]() 的二次函数,而二次函数的单调性与开口和对称轴有关,
的二次函数,而二次函数的单调性与开口和对称轴有关,
虽然![]() 能确定开口方向,但是不能确定对称轴的位置,故不能判断数列
能确定开口方向,但是不能确定对称轴的位置,故不能判断数列![]() 的单调性,故本命题是假命题;
的单调性,故本命题是假命题;
③:因为数列![]() 是等差数列,
是等差数列,
所以![]() ,
,
设![]() ,因此数列
,因此数列![]() 的通项公式为:
的通项公式为:![]() ,
,
显然当![]() 时,数列
时,数列![]() 是常数列,故本命题是假命题;
是常数列,故本命题是假命题;
④:因为数列![]() 是等差数列,
是等差数列,
所以![]() ,
,
设![]() ,因此数列
,因此数列![]() 的通项公式为
的通项公式为![]() ,
,
所以可以把![]() 看成关于
看成关于![]() 的一次函数,
的一次函数,
而![]() ,所以数列
,所以数列![]() 是递增数列,因此本命题是真命题.
是递增数列,因此本命题是真命题.
故选:B


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 |
| 84 | 83 | 80 | 75 | 68 |
已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;可供选择的数据:
;可供选择的数据:![]() ,
,![]() ;
;
(3)用![]() 表示用(2)中所求的线性回归方程得到的与
表示用(2)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数
称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(参考公式:线性回归方程中![]() 的最小二乘估计分别为
的最小二乘估计分别为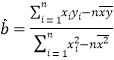 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程是:
的方程是: ![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设过原点的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左右焦点分别
的左右焦点分别![]()
![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线
轴的直线![]() 交椭圆于
交椭圆于![]() 两点,满足
两点,满足![]() .
.
(1)求椭圆![]() 的离心率.
的离心率.
(2)![]() 是椭圆
是椭圆![]() 短轴的两个端点,设点
短轴的两个端点,设点![]() 是椭圆
是椭圆![]() 上一点(异于椭圆
上一点(异于椭圆![]() 的顶点),直线
的顶点),直线![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 两点,
两点,![]() 为坐标原点,若
为坐标原点,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
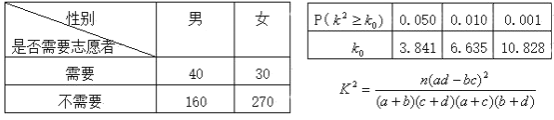
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在过点![]() 的直线
的直线![]() 与
与![]() 相交于不同的两点
相交于不同的两点![]() ,满足
,满足![]() ?
?
若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com