
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程是:
的方程是: ![]() ,以坐标原点为极点,
,以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设过原点的直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
(1)将直角坐标方程转化为极坐标方程可得曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(2)法1:由圆的弦长公式可得圆心![]() 到直线
到直线![]() 距离
距离![]() ,由几何关系可得直线
,由几何关系可得直线![]() 的斜率为
的斜率为![]() .
.
法2:设直线![]() :
: ![]() (
(![]() 为参数),与圆的直角坐标方程联立,利用直线参数的几何意义可得直线
为参数),与圆的直角坐标方程联立,利用直线参数的几何意义可得直线![]() 的斜率为
的斜率为![]() .
.
法3:设直线![]() :
: ![]() ,与圆的方程联立,结合圆锥曲线的弦长公式可得直线
,与圆的方程联立,结合圆锥曲线的弦长公式可得直线![]() 的斜率为
的斜率为![]() .
.
法4:设直线![]() :
: ![]() ,结合弦长公式可得圆心
,结合弦长公式可得圆心![]() 到直线
到直线![]() 距离
距离![]() ,利用点到直线距离公式解方程可得直线
,利用点到直线距离公式解方程可得直线![]() 的斜率为
的斜率为![]() .
.
试题解析:
(1)曲线![]() :
: ![]() ,即
,即![]() ,
,
将![]() ,
, ![]() 代入得
代入得
曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
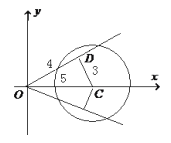
(2)法1:由圆的弦长公式![]() 及
及![]() ,得圆心
,得圆心![]() 到直线
到直线![]() 距离
距离![]() ,
,
如图,在![]() 中,易得
中,易得![]() ,可知
,可知
直线![]() 的斜率为
的斜率为![]() .
.
法2:设直线![]() :
: ![]() (
(![]() 为参数),代入
为参数),代入![]() 中得
中得![]() ,整理得
,整理得![]() ,
,
由![]() 得
得![]() ,即
,即![]() ,
,
解得![]() ,从而得直线
,从而得直线![]() 的斜率为
的斜率为![]() .
.
法3:设直线![]() :
: ![]() ,代入
,代入![]() 中得
中得
![]() ,即
,即![]() ,
,
由![]() 得
得![]() ,即
,即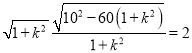 ,
,
解得直线![]() 的斜率为
的斜率为![]() .
.
法4:设直线![]() :
: ![]() ,则圆心
,则圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
由圆的弦长公式![]() 及
及![]() ,得圆心
,得圆心![]() 到直线
到直线![]() 距离
距离![]() ,
,
所以![]() ,解得直线
,解得直线![]() 的斜率为
的斜率为![]() .
.


科目:高中数学 来源: 题型:
【题目】小华与另外![]() 名同学进行“手心手背”游戏,规则是:
名同学进行“手心手背”游戏,规则是:![]() 人同时随机选择手心或手背其中一种手势,规定相同手势人数更多者每人得
人同时随机选择手心或手背其中一种手势,规定相同手势人数更多者每人得![]() 分,其余每人得
分,其余每人得![]() 分.现
分.现![]() 人共进行了
人共进行了![]() 次游戏,记小华
次游戏,记小华![]() 次游戏得分之和为
次游戏得分之和为![]() ,则
,则![]() 为( )
为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,点
,点![]() 是动点,且直线
是动点,且直线![]() 和直线
和直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 与(1)中轨迹相切于点
与(1)中轨迹相切于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,判断以
,判断以![]() 为直径的圆是否过
为直径的圆是否过![]() 轴上一定点?
轴上一定点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园有三条观光大道![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,斜边
,斜边![]() .现有甲、乙、丙三位小朋友分别在
.现有甲、乙、丙三位小朋友分别在![]() 大道上嬉戏,所在位置分别记为点
大道上嬉戏,所在位置分别记为点![]() .
.
(1)若甲乙都以每分钟![]() 的速度从点
的速度从点![]() 出发在各自的大道上奔走,到大道的另一端
出发在各自的大道上奔走,到大道的另一端
时即停,乙比甲迟2分钟出发,当乙出发1分钟后,求此时甲乙两人之间的距离;
(2)设![]() ,乙丙之间的距离是甲乙之间距离的2倍,且
,乙丙之间的距离是甲乙之间距离的2倍,且![]() ,请将甲
,请将甲
乙之间的距离![]() 表示为θ的函数,并求甲乙之间的最小距离.
表示为θ的函数,并求甲乙之间的最小距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的公差d>0,则下列四个命题:
的公差d>0,则下列四个命题:
①数列![]() 是递增数列; ②数列
是递增数列; ②数列![]() 是递增数列;
是递增数列;
③数列![]() 是递增数列; ④数列
是递增数列; ④数列![]() 是递增数列.
是递增数列.
其中正确命题的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,△ABC是等边三角形,AB⊥AD,CB⊥CD,点P是AC的中点,记△BPD、△ABD的面积分别为
中,△ABC是等边三角形,AB⊥AD,CB⊥CD,点P是AC的中点,记△BPD、△ABD的面积分别为![]() ,
,![]() ,二面角A-BD-C的大小为
,二面角A-BD-C的大小为![]() ,
,
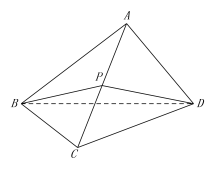
证明:(Ⅰ)平面ACD![]() 平面BDP;
平面BDP;
(Ⅱ)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,且
,且![]() (如图①).将四边形
(如图①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() 、
、![]() 、
、![]() (如图②).在折起的过程中,则下列表述:
(如图②).在折起的过程中,则下列表述:

①![]() 平面
平面![]() ;
;
②四点![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.其中正确的是__________.
可能垂直.其中正确的是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com