
【题目】(1)已知双曲线的中心在原点,焦点在x轴上,实轴长为4,渐近线方程为![]() .求双曲线的标准方程;
.求双曲线的标准方程;
(2)过(1)中双曲线上一点P的直线分别交两条渐近于![]() 两点,且P是线段AB的中点,求证:
两点,且P是线段AB的中点,求证:![]() 为常数;
为常数;
(3)我们知道函数![]() 的图象是由双曲线
的图象是由双曲线![]() 的图象逆时针旋转45°得到的,函数
的图象逆时针旋转45°得到的,函数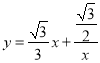 的图象也是双曲线,请尝试写出曲线
的图象也是双曲线,请尝试写出曲线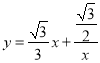 的性质(不必证明).
的性质(不必证明).
【答案】(1)![]() (2)证明见解析(3)详见解析
(2)证明见解析(3)详见解析
【解析】
(1)根据双曲线的性质求得双曲线的方程;
(2)方法一:设A,B点坐标,求得P点坐标,代入双曲线方程,即可求得![]() ;
;
方法二:分类讨论,设直线AB的方程,分别求得A和B点坐标,求得P点坐标,代入双曲线方程,即可求得![]() ;
;
(3)根据曲线方程,分别求得曲线的性质.
(1)设双曲线的方程为![]() ,由
,由![]() ,
,
由双曲线的渐近线方程为![]() ,则
,则![]() ,则
,则![]() ,
,
∴双曲线的方程为:![]() ;
;
(2)法一:由题不妨设![]() ,则
,则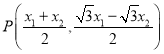 ,
,
则P在双曲线上,代入双曲线方程得![]()
法二:当直线AB的斜率不存在时,显然![]() ,则
,则![]() ;
;
当直线AB的斜率存在时,设直线AB的方程为![]()
则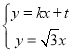 ,则
,则 ,
,
同理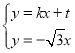 ,则
,则 ,
,
此时,![]() ,代入双曲线方程得
,代入双曲线方程得![]() ,则
,则![]()
(3)①对称中心:原点,对称轴方程:![]() ,
,
②顶点坐标为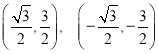 ,焦点坐标:
,焦点坐标:![]() ,
,![]() ,
,
实轴长:![]() ,虚轴长:2b=2,焦距:2c=4;
,虚轴长:2b=2,焦距:2c=4;
③范围:x≠0,![]() ,
,
④渐近线:![]() .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E,F分别是C1D1,CC1的中点,则异面直线AE与BF所成角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )

A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①在直角梯形ABCP中,![]() ,
,![]() ,
,![]() ,
,![]() ,E,F,G分别是线段PC,PD,BC的中点,现将
,E,F,G分别是线段PC,PD,BC的中点,现将![]() 折起,使平面
折起,使平面![]() 平面ABCD如图②.
平面ABCD如图②.
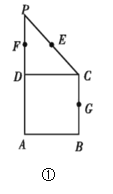
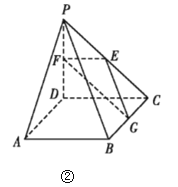
(1)求证:![]() 平面EFG;
平面EFG;
(2)求二面角G—EF—D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 为双曲线
为双曲线![]()
![]() 的左、右焦点,过
的左、右焦点,过![]() 作垂直于
作垂直于![]() 轴的直线,在
轴的直线,在![]() 轴上方交双曲线
轴上方交双曲线![]() 于点
于点![]() ,且
,且![]() ,圆
,圆![]() 的方程是
的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)过双曲线![]() 上任意一点
上任意一点![]() 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)过圆![]() 上任意一点
上任意一点![]() 作圆
作圆![]() 的切线
的切线![]() 交双曲线
交双曲线![]() 于
于![]() 、
、![]() 两点,
两点,![]() 中点为
中点为![]() ,求证:
,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某地出土的一种“钉”是由四条线段组成,其结构能使它任意抛至水平面后,总有一端所在的直线竖直向上,并记组成该“钉”的四条线段的公共点为O,钉尖为![]() .
.
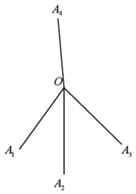
⑴设![]() ,当
,当![]() ,
,![]() ,
,![]() 在同一水平面内时,求
在同一水平面内时,求![]() 与平面
与平面![]() 所成角的大小
所成角的大小![]() 结果用反三角函数值表示
结果用反三角函数值表示![]() .
.
⑵若该“钉”的三个钉尖所确定的三角形的面积为![]() ,要用某种线型材料复制100枚这种“钉”
,要用某种线型材料复制100枚这种“钉”![]() 损耗忽略不计
损耗忽略不计![]() ,共需要该种材料多少米?
,共需要该种材料多少米?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,若对任意
,若对任意![]() ,满足
,满足![]() 且
且![]() (
(![]() 是与
是与![]() 无关的常数),则称数列
无关的常数),则称数列![]() 为
为![]() 数列.
数列.
(1)若![]() (
(![]() ),判断数列
),判断数列![]() 是否为
是否为![]() 数列,说明理由;
数列,说明理由;
(2)设![]() ,求证:数列
,求证:数列![]() 是
是![]() 数列,并求常数
数列,并求常数![]() 的取值范围;
的取值范围;
(3)设数列![]() (
(![]() ,
,![]() ),问数列
),问数列![]() 是否为
是否为![]() 数列?说明理由.
数列?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com