
【题目】已知函数![]() .
.
(Ⅰ)对任意的实数![]() ,恒有
,恒有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)在(Ⅰ)的条件下,当实数![]() 取最小值时,讨论函数
取最小值时,讨论函数![]() 在
在![]() 时的零点个数.
时的零点个数.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】
(Ⅰ)由![]() 可知,区间
可知,区间![]() 是不等式
是不等式![]() 解集的子集,由此可得出实数
解集的子集,由此可得出实数![]() 的不等式,解出即可;
的不等式,解出即可;
(Ⅱ)由题意可知,![]() ,则
,则![]() ,令
,令![]() ,可得出
,可得出![]() ,令
,令![]() ,对实数
,对实数![]() 的取值范围进行分类讨论,先讨论方程
的取值范围进行分类讨论,先讨论方程![]() 的根的个数及根的范围,进而得出方程
的根的个数及根的范围,进而得出方程![]() 的根个数,由此可得出结论.
的根个数,由此可得出结论.
(Ⅰ)![]() ,
,![]() ,
,
![]() 对任意的实数
对任意的实数![]() ,恒有
,恒有![]() 成立,
成立,
则区间![]() 是不等式
是不等式![]() 解集的子集,
解集的子集,![]() ,解得
,解得![]() ,
,
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(Ⅱ)![]() ,由题意可知,
,由题意可知,![]() ,
,![]() ,
,
令![]() ,得
,得![]() ,令
,令![]() ,
,
则![]() ,作出函数
,作出函数![]() 和函数
和函数![]() 在
在![]() 时的图象如下图所示:
时的图象如下图所示:
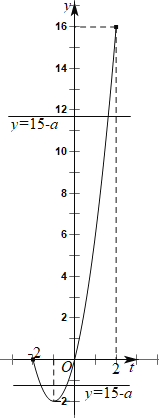
作出函数![]() 在
在![]() 时的图象如下图所示:
时的图象如下图所示:
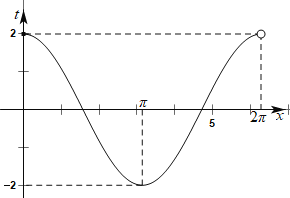
①当![]() 或
或![]() 时,即当
时,即当![]() 或
或![]() 时,方程
时,方程![]() 无实根,
无实根,
此时,函数![]() 无零点;
无零点;
②当![]() 时,即当
时,即当![]() 时,方程
时,方程![]() 的根为
的根为![]() ,
,
而方程![]() 在区间
在区间![]() 上有两个实根,此时,函数
上有两个实根,此时,函数![]() 有两个零点;
有两个零点;
③当![]() 时,即当
时,即当![]() 时,方程
时,方程![]() 有两根
有两根![]() 、
、![]() ,
,
且![]() ,
,![]() ,
,
方程![]() 在区间
在区间![]() 上有两个实根,方程
上有两个实根,方程![]() 在区间
在区间![]() 上有两个实根,此时,函数
上有两个实根,此时,函数![]() 有四个零点;
有四个零点;
④当![]() 时,即当
时,即当![]() 时,方程
时,方程![]() 有两根分别为
有两根分别为![]() 、
、![]() ,
,
方程![]() 在区间
在区间![]() 上只有一个实根,方程
上只有一个实根,方程![]() 在区间
在区间![]() 上有两个实根,此时,函数
上有两个实根,此时,函数![]() 有三个零点;
有三个零点;
⑤当![]() 时,即当
时,即当![]() 时,方程
时,方程![]() 只有一个实根
只有一个实根![]() ,且
,且![]() ,
,
方程![]() 在区间
在区间![]() 上有两个实根,此时,函数
上有两个实根,此时,函数![]() 有两个零点;
有两个零点;
⑥当![]() 时,即当
时,即当![]() 时,方程
时,方程![]() 只有一个实根
只有一个实根![]() ,
,
方程![]() 在区间
在区间![]() 上只有一个实根,此时,函数
上只有一个实根,此时,函数![]() 只有一个零点.
只有一个零点.
综上所述,当![]() 或
或![]() 时,函数
时,函数![]() 无零点;
无零点;
当![]() 时,函数
时,函数![]() 只有一个零点;
只有一个零点;
当![]() 或
或![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
当![]() 时,函数
时,函数![]() 有三个零点;
有三个零点;
当![]() 时,函数
时,函数![]() 有四个零点.
有四个零点.


科目:高中数学 来源: 题型:
【题目】一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,若两只蚂蚁均从点A(1,0)同时逆时针匀速爬动,若红蚂蚁每秒爬过α角,黑蚂蚁每秒爬过β角(其中0°<α<β<180°),如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求α,β的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点B是
的直径,点B是![]() 上与A,C不重合的动点,
上与A,C不重合的动点,![]() 平面
平面![]() .
.

(1)当点B在什么位置时,平面![]() 平面
平面![]() ,并证明之;
,并证明之;
(2)请判断,当点B在![]() 上运动时,会不会使得
上运动时,会不会使得![]() ,若存在这样的点B,请确定点B的位置,若不存在,请说明理由.
,若存在这样的点B,请确定点B的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的检验员为了检测生产线上生产零件的情况,从产品中随机抽取了![]() 个进行测量,根据所测量的数据画出频率分布直方图如下:
个进行测量,根据所测量的数据画出频率分布直方图如下:
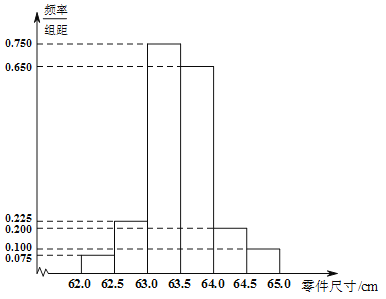
注:尺寸数据在![]() 内的零件为合格品,频率作为概率.
内的零件为合格品,频率作为概率.
(Ⅰ) 从产品中随机抽取![]() 件,合格品的个数为
件,合格品的个数为![]() ,求
,求![]() 的分布列与期望;
的分布列与期望;
(Ⅱ) 从产品中随机抽取![]() 件,全是合格品的概率不小于
件,全是合格品的概率不小于![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅲ) 为了提高产品合格率,现提出![]() 两种不同的改进方案进行试验.若按
两种不同的改进方案进行试验.若按![]() 方案进行试验后,随机抽取
方案进行试验后,随机抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() ;若按
;若按![]() 方案试验后,抽取
方案试验后,抽取![]() 件产品,不合格个数的期望是
件产品,不合格个数的期望是![]() ,你会选择哪个改进方案?
,你会选择哪个改进方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD-A1B1C1D1中(如图),AD=AA1=1,AB=2,点E是棱AB的中点.
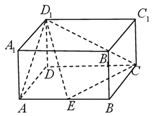
(1)求异面直线AD1与EC所成角的大小;
(2)《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,试问四面体D1CDE是否为鳖臑?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设要考察某公司生产的![]() 克袋装牛奶的质量是否达标,现从
克袋装牛奶的质量是否达标,现从![]() 袋牛奶中抽取
袋牛奶中抽取![]() 袋牛奶进行检验,利用随机数表抽样时,先将
袋牛奶进行检验,利用随机数表抽样时,先将![]() 袋牛奶按
袋牛奶按![]() 、
、![]() 、
、![]() 、
、![]() 进行编号,如果从随机数表第
进行编号,如果从随机数表第![]() 行第
行第![]() 列开始向右读,请你依次写出最先检测的
列开始向右读,请你依次写出最先检测的![]() 袋牛奶的编号_____________,_____________,_____________,_____________,_____________.(下面摘取了随机数表第
袋牛奶的编号_____________,_____________,_____________,_____________,_____________.(下面摘取了随机数表第![]() 行至第
行至第![]() 行)
行)
8842 1753 3157 2455 0688 7704 7476 7217 6335 0258 3921 2067 64
6301 6378 5916 9556 6719 9810 5071 7512 8673 5807 4439 5238 79
3321 1234 2978 6456 0782 5242 0744 3815 5100 1342 9966 0279 54
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体![]() 的长,宽,高分别为4,3,5,现有一甲壳虫从
的长,宽,高分别为4,3,5,现有一甲壳虫从![]() 点出发沿长方体表面爬行到
点出发沿长方体表面爬行到![]() 点来获取食物.
点来获取食物.
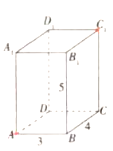
(1)甲壳虫想尽快获取食物可通过哪些路径获取?
(2)哪条获取食物的路径最短?最短为多少?
(3)此类问题的一般处理方法是什么?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:


(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;

(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人.
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
![]()
![]() ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com