
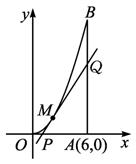
(1)试用t表示切线PQ的方程;
(2)设△QAP的面积为g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;
(3)试求g(t)的取值范围.
解:(1)设点M(t,t2),又f′(x)=2x,
∴过点M的切线PQ的斜率k=2t.
∴切线PQ的方程为y=2tx-t2.
(2)由(1)可求得P(![]() ,0)、Q(6,12t-t2),
,0)、Q(6,12t-t2),
∴g(t)=S△QAP=![]() (6-
(6-![]() t)(12t-t2)=
t)(12t-t2)=![]() -6t2+36t.
-6t2+36t.
由于g′(t)=![]() -12t+36,
-12t+36,
令g′(t)<0,则4<t<12,考虑到0<t<6,
∴4<t<6.
∴函数g(t)的单调递减区间是(4,6).
因此m的最小值为4.
(3)由(2)知,g(t)在区间(4,6)上递减,
∴此时S△QAP∈(g(6),g(4))=(54,64).
令g′(t)>0,则0<t<4,
∴g(t)在区间(0,4)上递增.
∴S△QAP∈(g(0),g(4))=(0,64).
又g(4)=64,
故g(t)的值域为(0,64].


科目:高中数学 来源: 题型:
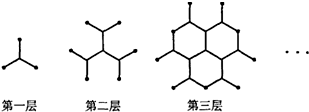 (2013•宁德模拟)一种平面分形图的形成过程如图所示,第一层是同 一点出发的三条线段,长度均为1,每两条线段夹角为 120°;第二层是在第一层的每一条线段末端,再生成 两条与该线段成120°角的线段,长度不变;第三层按 第二层的方法再在第二层每一条线段的末端各生成两条 线段;重复前面的作法,直至第6层,则分形图第6层 各条线段末端之间的距离的最大值为
(2013•宁德模拟)一种平面分形图的形成过程如图所示,第一层是同 一点出发的三条线段,长度均为1,每两条线段夹角为 120°;第二层是在第一层的每一条线段末端,再生成 两条与该线段成120°角的线段,长度不变;第三层按 第二层的方法再在第二层每一条线段的末端各生成两条 线段;重复前面的作法,直至第6层,则分形图第6层 各条线段末端之间的距离的最大值为| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:新课标高三数学函数专项训练(河北) 题型:填空题
设函数y=f(x)是最小正周期为2的偶函数,它在区间[0,1]上的图象为如图所示的线段AB,则在区间[1,2]上f(x)=______.
查看答案和解析>>
科目:高中数学 来源:2013届山东省济宁市高二3月月考理科数学试卷 题型:解答题
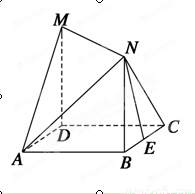
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点.
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN?若存在,求线段AS的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com