Question

【题目】已知函数，若不等式在上恒成立，则的最小值是（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

令h（x）f（x）﹣g（x）=lnx﹣（a﹣e）x﹣2b，利用导数求得h（x）max=h（）=﹣ln（a﹣e）﹣1﹣2b≤0，求得≥，a＞e，运用导数求得a=2e时，可得所求最小值．

由题意可知：在上恒成立，

构造函数，原问题等价于，

其中，

若，则恒成立，函数单调递增，不合题意，

据此可知，由导函数的符号可知：

函数在区间上单调递增，在区间上单调递减，

函数的最大值，

整理可得：，则，

构造函数，则，

原问题等价于求解函数的最大值.

由于，

故，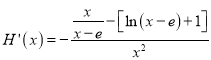

构造函数，

则，恒成立，则在定义域内单调递减，注意到，

故在区间上，函数，，单调递减，

故在区间上，函数，，单调递增，

函数的最大值为.

综上可得：的最小值是 .

故选：B.