
【题目】已知点A是以BC为直径的圆O上异于B,C的动点,P为平面ABC外一点,且平面PBC⊥平面ABC,BC=3,PB=2![]() ,PC
,PC![]() ,则三棱锥P﹣ABC外接球的表面积为______.
,则三棱锥P﹣ABC外接球的表面积为______.
 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() ,
,![]() ,
,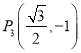 ,
,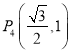 四点中恰有三点在椭圆
四点中恰有三点在椭圆![]() 上,抛物线
上,抛物线![]() 焦点到准线的距离为
焦点到准线的距离为![]() .
.
(1)求椭圆![]() 、抛物线
、抛物线![]() 的方程;
的方程;
(2)过椭圆![]() 右顶点Q的直线
右顶点Q的直线![]() 与抛物线
与抛物线![]() 交于点A、B,射线
交于点A、B,射线![]() 、
、![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() 、
、![]() .
.
(i)证明:![]() 为定值;
为定值;
(ii)记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() :
:![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)若![]() ,求直线的方程;
,求直线的方程;
(2)过点![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,若线段
两点,若线段![]() ,
,![]() 的中点分别为
的中点分别为![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求点
,求点![]() 到直线
到直线![]() 与
与![]() 距离和的最大值.
距离和的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张举办了一次抽奖活动.顾客花费3元钱可获得一次抽奖机会.每次抽奖时,顾客从装有1个黑球,3个红球和6个白球(除颜色外其他都相同)的不透明的袋子中依次不放回地摸出3个球,根据摸出的球的颜色情况进行兑奖.顾客中一等奖,二等奖,三等奖,四等奖时分别可领取的奖金为![]() 元,10元,5元,1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况:
元,10元,5元,1元.若经营者小张将顾客摸出的3个球的颜色分成以下五种情况:![]() 个黑球2个红球;
个黑球2个红球;![]() 个红球;
个红球;![]() 恰有1个白球;
恰有1个白球;![]() 恰有2个白球;
恰有2个白球;![]() 个白球,且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖,中二等奖,中三等奖,中四等奖,不中奖.
个白球,且小张计划将五种情况按发生的机会从小到大的顺序分别对应中一等奖,中二等奖,中三等奖,中四等奖,不中奖.
(1)通过计算写出中一至四等奖分别对应的情况(写出字母即可);
(2)已知顾客摸出的第一个球是红球,求他获得二等奖的概率;
(3)设顾客抽一次奖小张获利![]() 元,求变量
元,求变量![]() 的分布列;若小张不打算在活动中亏本,求
的分布列;若小张不打算在活动中亏本,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
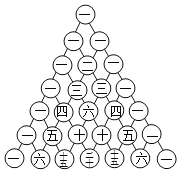
【题目】杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列,在我国南宋数学家杨辉所著的《评解九章算法》(![]() 年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:
年)一书中用如图所示的三角形解释二项式乘方展开式的系数规律,现把杨辉三角中的数从上到下,从左到右依次排列,得数列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …….记作数列
…….记作数列![]() ,若数列
,若数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棱长为1的正方体![]() 内部有一圆柱
内部有一圆柱![]() ,此圆柱恰好以直线
,此圆柱恰好以直线![]() 为轴.有下列命题:
为轴.有下列命题:
①圆柱![]() 的母线与正方体
的母线与正方体![]() 所有的棱所成的角都相等;
所有的棱所成的角都相等;
②正方体![]() 所有的面与圆柱
所有的面与圆柱![]() 的底面所成的角都相等;
的底面所成的角都相等;
③在正方体![]() 内作与圆柱
内作与圆柱![]() 底面平行的截面,则截面的面积
底面平行的截面,则截面的面积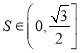 ;
;
④圆柱![]() 侧面积的最大值为
侧面积的最大值为![]() .
.
其中正确的命题是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把方程![]() 表示的曲线作为函数
表示的曲线作为函数![]() 的图象,则下列结论正确的是( )
的图象,则下列结论正确的是( )
①![]() 在R上单调递减
在R上单调递减
②![]() 的图像关于原点对称
的图像关于原点对称
③![]() 的图象上的点到坐标原点的距离的最小值为3
的图象上的点到坐标原点的距离的最小值为3
④函数![]() 不存在零点
不存在零点
A.①③B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=axex,g(x)=x2+2x+b,若曲线y=f(x)与曲线y=g(x)都过点P(1,c).且在点P处有相同的切线l.
(Ⅰ)求切线l的方程;
(Ⅱ)若关于x的不等式k[ef(x)]≥g(x)对任意x∈[﹣1,+∞)恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com