
【题目】设函数![]() ,
,![]() (
(![]() ).
).
(1)当![]() 时,解关于
时,解关于![]() 的方程
的方程![]() (其中
(其中![]() 为自然对数的底数);
为自然对数的底数);
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由. (参考数据:
的最小值;若不存在,请说明理由. (参考数据:![]() ,
,![]() )
)
【答案】(Ⅰ)![]() 或
或![]() (Ⅱ)当
(Ⅱ)当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;当
;当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;
;![]() 时,
时,![]() 的增区间为
的增区间为![]() .(III)
.(III)![]() 的最小值为
的最小值为![]() .
.
【解析】
试题分析:(Ⅰ)代入化简方程得![]() ,由二次方程解得
,由二次方程解得![]() 或
或![]() ,再根据指对数关系得
,再根据指对数关系得![]() 或
或![]() .(Ⅱ)先求函数导数并明确函数定义域:
.(Ⅱ)先求函数导数并明确函数定义域:![]() ,
,![]() ;再讨论导函数不变号情况:当
;再讨论导函数不变号情况:当![]() 时,
时,![]() ,
,![]() 的增区间为
的增区间为![]() ;最后讨论导函数变号时符号变化规律:当
;最后讨论导函数变号时符号变化规律:当![]() 时,由
时,由![]() ,解得
,解得![]() ;当
;当![]() 时,由
时,由![]() ,解得
,解得![]() .(III)存在性问题,一般转化为对应函数最值问题:
.(III)存在性问题,一般转化为对应函数最值问题:![]() ,利用导数先求函数
,利用导数先求函数![]() 最小值:本题难点是最小值点
最小值:本题难点是最小值点![]() 不能解出,只能得到其所在区间,为使
不能解出,只能得到其所在区间,为使![]() 值能确定最小值,需精确考虑最小值点所在区间,如
值能确定最小值,需精确考虑最小值点所在区间,如![]() 细化到
细化到![]()
试题解析:解:(1)当![]() 时,方程
时,方程![]() 即为
即为![]() ,去分母,得
,去分母,得
![]() ,解得
,解得![]() 或
或![]() , …………2分
, …………2分
故所求方程的根为![]() 或
或![]() . ………4分
. ………4分
(2)因为![]() ,
,
所以![]() (
(![]() ), ……6分
), ……6分
①当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
②当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
③当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
④当![]() 时,由
时,由![]() ,解得
,解得![]() ;
;
⑤当![]() 时,由
时,由![]() ,解得
,解得![]() .
.
综上所述,当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;
;
当![]() 时,
时,![]() 的增区间为
的增区间为![]() ;
;
![]() 时,
时,![]() 的增区间为
的增区间为![]() . ………10分
. ………10分
(3)方法一:当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 单调递增,
单调递增,![]() ,
,![]() ,
,
所以存在唯一![]() ,使得
,使得![]() ,即
,即![]() , ……………12分
, ……………12分
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() ,
,
记函数![]() ,则
,则![]() 在
在![]() 上单调递增, ……14分
上单调递增, ……14分
所以![]() ,即
,即![]() ,
,
由![]() ,且
,且![]() 为整数,得
为整数,得![]() ,
,
所以存在整数![]() 满足题意,且
满足题意,且![]() 的最小值为
的最小值为![]() . ………16分
. ………16分
方法二:当![]() 时,
时,![]() ,所以
,所以![]() ,
,
由![]() 得,当
得,当![]() 时,不等式
时,不等式![]() 有解, ……………12分
有解, ……………12分
下证:当![]() 时,
时,![]() 恒成立,即证
恒成立,即证![]() 恒成立.
恒成立.
显然当![]() 时,不等式恒成立,
时,不等式恒成立,
只需证明当![]() 时,
时,![]() 恒成立.
恒成立.
即证明![]() .令
.令![]() ,
,
所以![]() ,由
,由![]() ,得
,得![]() , ………14分
, ………14分
当![]() ,
,![]() ;当
;当![]() ,
,![]() ;
;
所以![]() .
.
所以当![]() 时,
时,![]() 恒成立.
恒成立.
综上所述,存在整数![]() 满足题意,且
满足题意,且![]() 的最小值为
的最小值为![]() . .……………16分
. .……………16分


科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上任意一点
上任意一点![]() 到直线
到直线![]() :
:![]() 的距离是它到点
的距离是它到点![]() 距离的2倍;曲线
距离的2倍;曲线![]() 是以原点为顶点,
是以原点为顶点,![]() 为焦点的抛物线.
为焦点的抛物线.
(1)求![]() ,
,![]() 的方程;
的方程;
(2)设过点![]() 的动直线与曲线
的动直线与曲线![]() 相交于
相交于![]() ,
,![]() 两点,分别以
两点,分别以![]() ,
,![]() 为切点引曲线
为切点引曲线![]() 的两条切线
的两条切线![]() ,
,![]() ,设
,设![]() ,
,![]() 相交于点
相交于点![]() .连接
.连接![]() 的直线交曲线
的直线交曲线![]() 于
于![]() ,
,![]() 两点.
两点.
(i)求证:![]() ;
;
(ii)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为做好创建国家生态文明单位的需要,某地甲、乙两大型企业决定先从本企业的所有员工中随机抽取8名员工,对自己所在企业的生态文明建设状况进行自我内部的评分调查(满分100分),被抽取的员工的评分结果如右表:
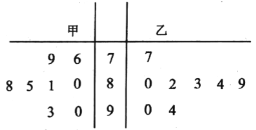
(1)若分别从甲、乙两企业被抽取的8名员工中各抽取1名,在已知两人中至少一人评分不低于80分的条件下,求抽到的甲企业员工评分低于80分的概率;
(2)用样本的频率分布估计总体的概率分布,若从甲企业的所有员工中,再随机抽取4名员工进行评分细节调查,记抽取的这4名员工中评分不低于90分的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】11月,2019全国美丽乡村篮球大赛在中国农村改革的发源地-安徽凤阳举办,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮),在相同的条件下,每轮甲乙两人在同一位置,甲先投,每人投一次球,两人有1人命中,命中者得1分,未命中者得-1分;两人都命中或都未命中,两人均得0分,设甲每次投球命中的概率为![]() ,乙每次投球命中的概率为
,乙每次投球命中的概率为![]() ,且各次投球互不影响.
,且各次投球互不影响.
(1)经过1轮投球,记甲的得分为![]() ,求
,求![]() 的分布列;
的分布列;
(2)若经过![]() 轮投球,用
轮投球,用![]() 表示经过第
表示经过第![]() 轮投球,累计得分,甲的得分高于乙的得分的概率.
轮投球,累计得分,甲的得分高于乙的得分的概率.
①求![]() ;
;
②规定![]() ,经过计算机计算可估计得
,经过计算机计算可估计得![]() ,请根据①中
,请根据①中![]() 的值分别写出a,c关于b的表达式,并由此求出数列
的值分别写出a,c关于b的表达式,并由此求出数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交50元,啤酒根据需要自己用量杯量取.结账时,剩余酒量不足1升的,按0升计算(如剩余1.7升,记为剩余1升).
![]()
统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的5组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求由这5组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了5位朋友一同来饮酒,小王及朋友用量杯共量取了8升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请一个或两个朋友一起来饮酒,会更划算.试问小王是否该接受服务生的建议.
参考数据:回归直线的方程是![]() ,其中
,其中
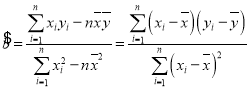 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() ,且直线
,且直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)设![]() 为原点,
为原点,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年“一带一路”沿线64个国家GDP之和约为12.0万亿美元,占全球GDP的![]() ;人口总数约为32.1亿,占全球总人口的
;人口总数约为32.1亿,占全球总人口的![]() ;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的
;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的![]() .
.
2016年“一带一路”沿线国家情况
人口(万人) | GDP(亿美元) | 进口额(亿美元) | 出口额(亿美元) | |
蒙古 | 301.4 | 116.5 | 38.7 | 45.0 |
东南亚11国 | 63852.5 | 25802.2 | 11267.2 | 11798.6 |
南亚8国 | 174499.0 | 29146.6 | 4724.1 | 3308.5 |
中亚5国 | 6946.7 | 2254.7 | 422.7 | 590.7 |
西亚、北非19国 | 43504.6 | 36467.5 | 9675.5 | 8850.7 |
东欧20国 | 32161.9 | 26352.1 | 9775.5 | 11388.4 |
关于“一带一路”沿线国家2016年状况,能够从上述资料中推出的是( )
A.超过六成人口集中在南亚地区
B.东南亚和南亚国家GDP之和占全球的![]() 以上
以上
C.平均每个南亚国家对外贸易额超过1000亿美元
D.平均每个东欧国家的进口额高于平均每个西亚、北非国家的进口额
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com