
【题目】狄利克雷是19世纪德国著名的数学家,他定义了一个“奇怪的函数” ,下列关于狄利克雷函数的叙述正确的有:______.
,下列关于狄利克雷函数的叙述正确的有:______.
①![]() 的定义域为
的定义域为![]() ,值域是
,值域是![]() ②
②![]() 具有奇偶性,且是偶函数
具有奇偶性,且是偶函数
③![]() 是周期函数,但它没有最小正周期 ④对任意的
是周期函数,但它没有最小正周期 ④对任意的![]() ,
,![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下图是某地区2009年至2018年芯片产业投资额![]() (单位:亿元)的散点图,为了预测该地区2019年的芯片产业投资额,建立了
(单位:亿元)的散点图,为了预测该地区2019年的芯片产业投资额,建立了![]() 与时间变量
与时间变量![]() 的四个线性回归模型.根据2009年至2018年的数据建立模型①;根据2010年至2017年的数据建立模型②;根据2011年至2016年的数据建立模型③;根据2014年至2018年的数据建立模型④.则预测值更可靠的模型是( )
的四个线性回归模型.根据2009年至2018年的数据建立模型①;根据2010年至2017年的数据建立模型②;根据2011年至2016年的数据建立模型③;根据2014年至2018年的数据建立模型④.则预测值更可靠的模型是( )

A.①B.②C.③D.④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),等腰梯形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的两个三等分点,若把等腰梯形沿虚线
的两个三等分点,若把等腰梯形沿虚线![]() 、
、![]() 折起,使得点
折起,使得点![]() 和点
和点![]() 重合,记为点
重合,记为点![]() , 如图(2).
, 如图(2).

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点O为坐标原点,椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,离心率为
(a>b>0)的左、右焦点分别为F1,F2,离心率为![]() ,点I,J分别是椭圆C的右顶点、上顶点,△IOJ的边IJ上的中线长为
,点I,J分别是椭圆C的右顶点、上顶点,△IOJ的边IJ上的中线长为![]() .
.
(1)求椭圆C的标准方程;
(2)过点H(-2,0)的直线交椭圆C于A,B两点,若AF1⊥BF1,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图),
(如图),![]() 为
为![]() 中点.
中点.
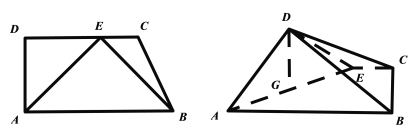
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,点M、N分别在AB1、BC1上,且AM=![]() AB1,BN=
AB1,BN=![]() BC1,则下列结论:①AA1⊥MN;②A1C1// MN;③MN//平面A1B1C1D1;④B1D1⊥MN,其中,
BC1,则下列结论:①AA1⊥MN;②A1C1// MN;③MN//平面A1B1C1D1;④B1D1⊥MN,其中,
正确命题的个数是( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁分店销售某种商品,该商品每件的进价为![]() 元,预计当每件商品售价为
元,预计当每件商品售价为![]() 元时,一年的销售量(单位:万件)
元时,一年的销售量(单位:万件) 该分店全年需向总店缴纳宣传费、保管费共计
该分店全年需向总店缴纳宣传费、保管费共计![]() 万元.
万元.
(1)求该连锁分店一年的利润与每件商品售价![]() 的函数关系式
的函数关系式![]() ;
;
(2)求当每件商品售价为多少元时,该连锁店一年的利润最大,并求其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从抛物线![]() 上任意一点P向x轴作垂线段,垂足为Q,点M是线段
上任意一点P向x轴作垂线段,垂足为Q,点M是线段![]() 上的一点,且满足
上的一点,且满足![]()
(1)求点M的轨迹C的方程;
(2)设直线![]() 与轨迹c交于
与轨迹c交于![]() 两点,T为C上异于
两点,T为C上异于![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() 两点,以
两点,以![]() 为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
为直径的圆是否过x轴上的定点?若过定点,求出符合条件的定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与椭圆
与椭圆![]() 相交于点M(0,1),N(0,-1),且椭圆的离心率为
相交于点M(0,1),N(0,-1),且椭圆的离心率为![]() .
.

(1)求![]() 的值和椭圆C的方程;
的值和椭圆C的方程;
(2)过点M的直线![]() 交圆O和椭圆C分别于A,B两点.
交圆O和椭圆C分别于A,B两点.
①若![]() ,求直线
,求直线![]() 的方程;
的方程;
②设直线NA的斜率为![]() ,直线NB的斜率为
,直线NB的斜率为![]() ,问:
,问:![]() 是否为定值? 如果是,求出定值;如果不是,说明理由.
是否为定值? 如果是,求出定值;如果不是,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com