Question

【题目】平面直角坐标系xOy中，椭圆C：＋＝1 (a>b>0)的离心率是，抛物线E：x2＝2y的焦点F是C的一个顶点．

(1)求椭圆C的方程；

(2)设P是E上的动点，且位于第一象限，E在点P处的切线l与C交于不同的两点A，B，线段AB的中点为D.直线OD与过P且垂直于x轴的直线交于点M.

①求证：点M在定直线上；

②直线l与y轴交于点G，记△PFG的面积为S1，△PDM的面积为S2，求的最大值及取得最大值时点P的坐标．

Answer 1

【答案】（1）；（2）①证明见解析；②的最大值为，此时点P的坐标为.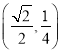

【解析】试题分析：(1)利用离心率、抛物线的焦点进行求解；(2)①设出点的坐标和直线的方程，联立直线和椭圆的方程，得到关于的一元二次方程，利用根与系数的关系进行求解；②利用点到直线的距离公式、弦长公式和函数的性质进行求解.

试题解析：(1)由题意知＝，

可得a2＝4b2，因为抛物线E的焦点为F，所以b＝，a＝1，

所以椭圆C的方程为x2＋4y2＝1.

(2)①证明　设P (m>0)，由x2＝2y，可得y′＝x，所以直线l的斜率为m，因此直线l的方程为y－＝m(x－m)，

即y＝mx－.

设A(x1，y1)，B(x2，y2)，D(x0，y0)．

联立方程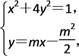

得(4m2＋1)x2－4m3x＋m4－1＝0.

由Δ>0，得0<m< (或0<m2<2＋)．(*)

且x1＋x2＝，因此x0＝，将其代入y＝mx－，

得y0＝，因为＝－.

所以直线OD的方程为y＝－x，

联立方程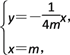

得点M的纵坐标yM＝－，

所以点M在定直线y＝－上．

②由①知直线l的方程为y＝mx－，令x＝0，得y＝－，

所以G，

又P，F，D，

所以S1＝·|GF|·m＝，

S2＝·|PM|·|m－x0|＝××＝，

所以＝.

设t＝2m2＋1，则＝

＝＝－＋＋2，

当＝，即t＝2时，取到最大值，

此时m＝，满足(*)式，所以P点坐标为.

因此的最大值为，此时点P的坐标为.