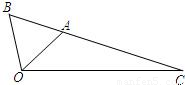
分析:(1)由已知易得
•的夹角为∠B的补角,由正弦定理,结合△OAC中,
OC=,∠OAC=120°,∠AOC=45°,∠OCA=15°,解三角形OAC,易得OB,BC的长,代入向量数量积公式即可求解.
(2)由D是线段BC上的任意点,若
=x
+y
,我们易得x+y=1,(其中0≤x≤1,0≤y≤1),构造函数f(x)=x
2y利用导数法确定函数的单调性,进而可求出x
2y的最大值.
解答: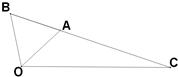
解:(1)
sin15o=sin(45o-30o)=(1分)
在△OAC中,∠OAC=120°,∠AOC=45°,∠OCA=15°,
∴
==,
即
===(3分)
故
OA=sin15o=×=1-,
AC=sin45o=×=,
∵OA=AB=OB=
1-,
故BC=AC+AB=
1+(5分)
∠OBC=60°,可得<
,
>=120°,
∴
•=(1-
)×(1+
)×cos120°=-
(7分)
(2)∵D、B、C三点共线,故可设
=λ
,(0≤λ≤1)(8分)
=(1-λ)
+λ
,又
=y
+x
,
故x+y=λ+(1-λ)=1,(其中0≤x≤1,0≤y≤1)(10分)
令f(x)=x
2y=x
2(1-x)=x
2-x
3(0≤x≤1)(11分)
f'(x)=2x-3x
2x∈[0,]时,f'(x)=2x-3x
2≥0?f(x)在区间
[0,]单调递增,
x∈[,1]时,f'(x)=2x-3x
2≤0?f(x)在区间
[,1]单调递减,(13分)
∴
fmax(x)=f()=,即x
2y的最大值为
.(14分)
点评:本题考查的知识是正弦定理,平面向量的数量积,三点共线的坐标表示,导数法求函数在定区间上的最值.其中(1)中利用正弦定理解三角形,(2)中根据D、B、C三点共线,得到x+y=1,(其中0≤x≤1,0≤y≤1),是解答的关键.

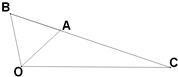 如图,△OAB是等边三角形,∠AOC=45°,OC=
如图,△OAB是等边三角形,∠AOC=45°,OC= 解:(1)sin15o=sin(45o-30o)=
解:(1)sin15o=sin(45o-30o)=

 快捷英语周周练系列答案
快捷英语周周练系列答案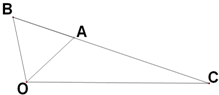 如图,△OAB是等边三角形,∠AOC=45°,OC=
如图,△OAB是等边三角形,∠AOC=45°,OC=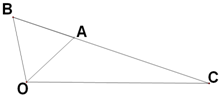
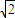 ,A、B、C三点共线.
,A、B、C三点共线.