
【题目】在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】分析:△ABC中设AB=c,BC=a,AC=b,由sinB=cosAsinC结合三角形的内角和及和角的正弦公式化简可求 cosC=0 即C=90°,再由![]() ,S△ABC=6可得bccosA=9,
,S△ABC=6可得bccosA=9,![]() 可求得c=5,b=3,a=4,考虑建立以AC所在的直线为x轴,以BC所在的直线为y轴建立直角坐标系,由P为线段AB上的一点,则存在实数λ使得
可求得c=5,b=3,a=4,考虑建立以AC所在的直线为x轴,以BC所在的直线为y轴建立直角坐标系,由P为线段AB上的一点,则存在实数λ使得![]() =(3λ,4﹣4λ)(0≤λ≤1),设
=(3λ,4﹣4λ)(0≤λ≤1),设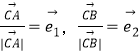 则
则![]() ,
,![]() ,由
,由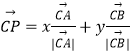 =(x,0)+(0,y)=(x,y)可得x=3λ,y=4﹣4λ则4x+3y=12而
=(x,0)+(0,y)=(x,y)可得x=3λ,y=4﹣4λ则4x+3y=12而![]() ,利用基本不等式求解最小值.
,利用基本不等式求解最小值.
详解:△ABC中设AB=c,BC=a,AC=b
∵sinB=cosAsinC,∴sin(A+C)=sinCcosA,
即sinAcosC+sinCcosA=sinCcosA,
∴sinAcosC=0,
∵sinA≠0,∴cosC=0 C=90°
∵![]() ,S△ABC=6
,S△ABC=6
∴bccosA=9,![]()
∴![]() ,根据直角三角形可得sinA=
,根据直角三角形可得sinA=![]() ,cosA=
,cosA=![]() ,bc=15
,bc=15
∴c=5,b=3,a=4
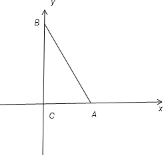
以AC所在的直线为x轴,以BC所在的直线为y轴建立直角坐标系可得C(0,0)A(3,0)B(0,4)
P为线段AB上的一点,则存在实数λ使得![]() =(3λ,4﹣4λ)(0≤λ≤1)
=(3λ,4﹣4λ)(0≤λ≤1)
设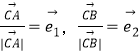 ,则
,则![]() ,
,![]()
∴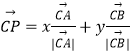 =(x,0)+(0,y)=(x,y)
=(x,0)+(0,y)=(x,y)
∴x=3λ,y=4﹣4λ则4x+3y=12
![]() =
=![]()
故所求的最小值为![]()
故选:C.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,且直线
,且直线![]() 是其图象的一条对称轴.
是其图象的一条对称轴.
(1)求函数![]() 的解析式;
的解析式;
(2)在![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别为
所对的边分别为![]() 、
、![]() 、
、![]() ,且
,且![]() ,
,![]() ,若
,若![]() 角满足
角满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的
个单位,再将所得的图象上每一点的纵坐标不变,横坐标伸长为原来的![]() 倍后所得到的图象对应的函数记作
倍后所得到的图象对应的函数记作![]() ,已知常数
,已知常数![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 内恰有
内恰有![]() 个零点,求常数
个零点,求常数![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于命题![]() :存在一个常数
:存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() 恒成立.
恒成立.
(1)试给出这个常数![]() 的值;
的值;
(2)在(1)所得结论的条件下证明命题![]() ;
;
(3)对于上述命题,某同学正确地猜想了命题![]() :“存在一个常数
:“存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() ,
,![]() 恒成立.”观察命题
恒成立.”观察命题![]() 与命题
与命题![]() 的规律,请猜想与正数
的规律,请猜想与正数![]() ,
,![]() ,
,![]() ,
,![]() 相关的命题.
相关的命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图231所示.
 图231
图231
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
(2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望E(X)及方差D(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() ,点
,点![]() 为曲线
为曲线![]() 上任意一点且满足
上任意一点且满足![]()
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() 是曲线
是曲线![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别交直线
分别交直线![]() :
:![]() 于点
于点![]() ,试问
,试问![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=xlnx﹣ax,g(x)=﹣x2﹣2.
(1)对一切x∈(0,+∞),f(x)≥g(x)恒成立,求实数a的取值范围;
(2)当a=﹣1时,求函数f(x)在区间[m,m+3](m>0)上的最值;
(3)证明:对一切x∈(0,+∞),都有 ![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产厂家生产一种产品的固定成本为4万元,并且每生产1百台产品需增加投入0.8万元.已知销售收入![]() (万元)满足
(万元)满足![]() (其中
(其中![]() 是该产品的月产量,单位:百台),假定生产的产品都能卖掉,请完成下列问题:
是该产品的月产量,单位:百台),假定生产的产品都能卖掉,请完成下列问题:
(1)将利润表示为月产量![]() 的函数
的函数![]() ;
;
(2)当月产量为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.

(1)求该几何体的体积![]() ;
;
(2)求该几何体的表面积![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com