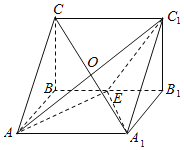
【题目】如图，直三棱柱
中，
，
，
，侧面
中心为O，点E是侧棱
上的一个动点，有下列判断，正确的是（ ）
A.直三棱柱侧面积是
B.直三棱柱体积是
C.三棱锥
的体积为定值D.
的最小值为
【答案】ACD
【解析】
由题意画出图形，计算直三棱柱的侧面积和体积即可判断A与B；由棱锥底面积与高为定值判断C；设BE＝x，列出AE+EC1关于x的函数式，结合其几何意义求出最小值判断D．
在直三棱柱
中，
，
，
底面
和
是等腰直角三角形，侧面全是矩形，所以其侧面积为1×2×2+
，故A正确；
直三棱柱的体积为
，故B不正确；
由BB1∥平面AA1C1C，且点E是侧棱
上的一个动点，
三棱锥
的高为定值
，
×
×2＝，
××＝
，故C正确；
设BE＝x
，则B1E＝2﹣x，在
和
中，∴
＝
．由其几何意义，
即平面内动点（x，1）与两定点（0，0），（2，0）距离和的最小值，由对称可知，当
为的中点时，其最小值为
，故D正确．
故选：ACD．
口算小状元口算速算天天练系列答案科目：高中数学 来源： 题型：
【题目】对于定义在区间D上的函数
，若存在正整数k，使不等式
恒成立，则称为
型函数.
（1）设函数
，定义域
.若是
型函数，求实数a的取值范围；
（2）设函数
，定义域
.判断
是否为
型函数，并给出证明.
（参考数据：
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某台函数计算器上有一个显示屏和两个操作键．若按一下第一个操作键，则将原显示屏上的数变为
（
表示不超过实数x的最大整数）；若按一下第二个操作键，则将原显示屏上的数变为
．称按一下任意一个操作键为一次操作．现在显示屏上的数为1．问：
（1）是否可以经过有限次操作，显示屏上出现整数2000？说明理由．
（2）小于2000的整数中有多少个数可以经过有限次操作在显示屏上出现？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
的三边长分别为a，b，c，其面积为S，则的内切圆O的半径
.这是一道平面几何题，其证明方法采用“等面积法”设空间四面体
四个面的面积分别为积为V，内切球半径为R.请用类比推理方法猜测对空间四面体存在类似结论为______.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《周髀算经》中给出了弦图，所谓弦图是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形，若图中直角三角形两锐角分别为
，
，且小正方形与大正方形面积之比为
，则
的值为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
（e为自然对数的底数，e≈2.718）．对于任意的
(0，e)，在区间(0，e)上总存在两个不同的
，
，使得
＝
＝
，则整数a的取值集合是_______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
