
【题目】已知两个不相等的非零向量![]() ,
,![]() ,两组向量
,两组向量![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均由2个
均由2个![]() 和3个
和3个![]() 排列而成,记
排列而成,记![]() ,
,![]() 表示S所有可能取值中的最小值,则下列命题中真命题的序号是________.(写出所有真命题的序号)
表示S所有可能取值中的最小值,则下列命题中真命题的序号是________.(写出所有真命题的序号)
①S有5个不同的值;②若![]() ,则
,则![]() 与
与![]() 无关;③若
无关;③若![]() ,则
,则![]() 与
与![]() 无关;
无关;
④若![]() ,则
,则![]() ;⑤若
;⑤若![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角为
的夹角为![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】对于一个向量组![]() ,令
,令![]() ,如果存在
,如果存在![]() ,使得
,使得![]() ,那么称
,那么称![]() 是该向量组的“长向量”
是该向量组的“长向量”
(1)若![]() 是向量组
是向量组![]() 的“长向量”,且
的“长向量”,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)已知![]() ,
,![]() ,
,![]() 均是向量组
均是向量组![]() 的“长向量”,试探究
的“长向量”,试探究![]() ,
,![]() ,
,![]() 的等量关系并加以证明.
的等量关系并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的面积为
的面积为![]() .
.
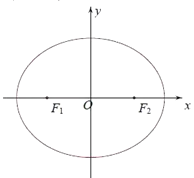
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 点的坐标;若不存在,请说明理由;
点的坐标;若不存在,请说明理由;
(3)设![]() 为椭圆
为椭圆![]() 上非长轴顶点的任意一点,
上非长轴顶点的任意一点,![]() 为线段
为线段![]() 上一点,若
上一点,若![]() 与
与![]() 的内切圆面积相等,求证:线段
的内切圆面积相等,求证:线段![]() 的长度为定值.
的长度为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() 曲线
曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,
,![]() 与
与![]() 轴的交点为
轴的交点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,如图1.已知
,如图1.已知![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() .
.


(1)求抛物线![]() 的方程;
的方程;
(2)若正方形![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() 都在抛物线
都在抛物线![]() 上(如图2),求正方形
上(如图2),求正方形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在![]() 内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为
内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).

(1)求选取的市民年龄在![]() 内的人数;
内的人数;
(2)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南方智运汽车公司在我市推出了共享汽车“Warmcar”,有一款车型为“众泰云”新能源共享汽车,其中一种租用方式“分时计费”规则为:0.15元/分钟+0.8元/公里.已知小李家离上班地点为10公里,每天租用该款汽车上、下班各一次,由于堵车、及红绿灯等原因每次路上开车花费的时间![]() (分钟)是一个随机变量,现统计了100次路上开车花费时间,在各时间段内是频数分布情况如下表所示:
(分钟)是一个随机变量,现统计了100次路上开车花费时间,在各时间段内是频数分布情况如下表所示:
时间 |
|
|
|
|
|
|
|
频数 | 2 | 6 | 14 | 36 | 28 | 10 | 4 |
(1)写出小李上班一次租车费用![]() (元)与用车时间
(元)与用车时间![]() (分钟)的函数关系;
(分钟)的函数关系;
(2)根据上面表格估计小李平均每次租车费用;
(3)“众泰云”新能源汽车还有一种租用方式为“按月计费”,规则为每个月收取租金2350元,若小李每个月上班时间平均按21天计算,在不计电费和情况下,请你为小李选择一种省钱的租车方式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①若线性回归方程为![]() ,则当变量
,则当变量![]() 增加一个单位时,
增加一个单位时,![]() 一定增加3个单位;②将一组数据中的每个数据都加上同一个常数后,方差不会改变;③线性回归直线方程
一定增加3个单位;②将一组数据中的每个数据都加上同一个常数后,方差不会改变;③线性回归直线方程![]() 必过点
必过点![]() ;④抽签法属于简单随机抽样;其中错误的说法是( )
;④抽签法属于简单随机抽样;其中错误的说法是( )
A.①③B.②③④C.①D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com