Question

【题目】已知命题p:函数f(x)=|2x+3c|在[-1,+∞)上单调递增;命题q:函数g(x)=+2有零点.

(1)若命题p和q均为真命题,求实数c的取值范围;

(2)是否存在实数c,使得p∧(q)是真命题?若存在,求出c的取值范围;若不存在,说明理由.

Answer 1

【答案】（1）；（2）

【解析】

(1)将f（x）转化成分段函数的形式，易得出f（x）的递增区间，结合[-1,+∞)上单调递增，再结合g（x）=0有解，求得c的取值范围.

(2) 使p∧ (q)是真命题,应使p真q假,得不等式组，解得c的取值范围.

因为f(x)=|2x+3c|=

所以f(x)的单调递增区间是.

又因为f(x)在[-1,+∞)上单调递增,

所以-≤-1,解得c≥.

因为函数g(x)=+2有零点,

所以方程+2=0有实数根,

即2x2+cx+2=0有实数根,

所以c2-16≥0,解得c≥4或c≤-4.

(1)当命题p和q均为真命题时,

应有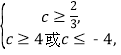即c≥4.

故c的取值范围是[4,+∞).

(2)要使p∧ (q)是真命题,应使p真q假,

因此有

解得≤c<4,

故存在实数c,使得p∧ (q)是真命题,其取值范围是.