
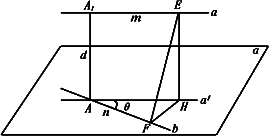
已知两条异面直线a,b所成的角为![]() ,它们的公垂线段AA1的长度为d,在直线a、b上分别取点E、F,设A1E=m,AF=n.求证:EF=
,它们的公垂线段AA1的长度为d,在直线a、b上分别取点E、F,设A1E=m,AF=n.求证:EF=![]()
科目:高中数学 来源: 题型:
| π |
| 3 |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
已知两条异面直线a和b分别是在平面α和β内,且α β=c,则
β=c,则
[ ]
A.直线c同时和a、b相交
B.直线c和a、b都不相交
C.直线c至少与a、b中的一条相交
D.直线c至少与a、b中的一条平行
查看答案和解析>>
科目:高中数学 来源: 题型:013
已知两条异面直线
a和b分别是在平面α和β内,且α β=c,则
β=c,则
[
]A
.直线c同时和a、b相交B
.直线c和a、b都不相交C
.直线c至少与a、b中的一条相交D
.直线c至少与a、b中的一条平行查看答案和解析>>
科目:高中数学 来源: 题型:
A.直线c同时和a、b相交
B.直线c和a、b都不相交
C.直线c至少和a、b中的一条相交
D.直线c至多和a、b中的一条相交
查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第83课时):第九章 直线、平面、简单几何体-立体几何小结(解析版) 题型:选择题
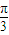 ,直线l与a,直线l与b所成的角为θ,则θ的范围是( )
,直线l与a,直线l与b所成的角为θ,则θ的范围是( )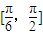


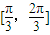
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com