练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一个正三棱柱的三视图如图所示，若该三棱柱的外接球的表面积为，则侧视图中的的值为 （ ）

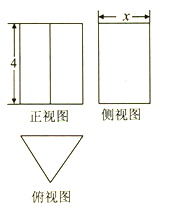
    A. 6 B. 4 C. 3 D. 2

    【答案】C

    【解析】分析：首先通过观察几何体的三视图，还原几何体，得知其为一个正三棱柱，结合直三棱柱的外接球的球心在上下底面外心连线的中点处，利用外接球的表面积，得到底面边长所满足的关系式，求得其边长，再根据侧视图中对应的边长与底面边长的关系，求得结果.

    详解：根据题中所给的几何体的三视图，可以得到该几何体是一个正三棱柱，

    设其底面边长为，则底面正三角形的外接圆的半径为，

    设该三棱锥的外接球的半径为R，

    结合正三棱锥的外接球的球心在上下底面的外心连线的中点处，

    则有，因为该三棱柱的外接球的表面积为，

    则有，从而解得，

    因为侧视图中对应的边为底面三角形的边的中线，

    求得，故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】苏格兰数学家纳皮尔发明了对数表，这一发明为当时的天文学家处理“大数运算”做出了巨大贡献法国著名数学家和天文学家拉普拉斯曾说过：“对数倍增了天文学家的寿命”比如在下面的部分对数表中，16，256对应的幂指数分别为4，8，幂指数和为12，而12对应的幂4096，因此根据此表，推算（ ）

    x

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    2

    4

    8

    16

    32

    64

    128

    256

    512

    1024

    x

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    2048

    4096

    8192

    16384

    32768

    65536

    131072

    262144

    524288

    1048576

    x

    21

    22

    23

    24

    25

    2097152

    4194304

    8388608

    16777216

    33554432

    A. 524288 B. 8388608 C. 16777216 D. 33554432

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是椭圆的左、右焦点，为坐标原点，点在椭圆上，线段与轴的交点满足．

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）圆是以为直径的圆，一直线与圆相切，并与椭圆交于不同的两点、，当，且满足时，求的面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（为常数），函数，（为常数，且）.

    （1）若函数有且只有1个零点，求的取值的集合.

    （2）当（1）中的取最大值时，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市根据地理位置划分成了南北两区，为调查该市的一种经济作物（下简称 作物）的生长状况，用简单随机抽样方法从该市调查了 500 处 作物种植点，其生长状况如表：

    其中生长指数的含义是：2 代表“生长良好”，1 代表“生长基本良好”，0 代表“不良好，但仍有收成”，﹣1代表“不良好，绝收”．

    （1）估计该市空气质量差的作物种植点中，不绝收的种植点所占的比例；

    （2）能否有 99%的把握认为“该市作物的种植点是否绝收与所在地域有关”？

    （3）根据（2）的结论，能否提供更好的调查方法来估计该市作物的种植点中，绝收种植点的比例？请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数角度看，可以看成是以为自变量的函数，其定义域是.

    （1）证明：

    （2）试利用1的结论来证明：当为偶数时，的展开式最中间一项的二项式系数最大；当为奇数时的展开式最中间两项的二项式系数相等且最大.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在集合中，任取个元素构成集合. 若的所有元素之和为偶数，则称为的偶子集，其个数记为；若的所有元素之和为奇数，则称为的奇子集，其个数记为. 令

    (1)当 时，求的值；

    (2)求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点为，圆：与轴的一个交点为，圆的圆心为，为等边三角形.

    求抛物线的方程；

    设圆与抛物线交于两点，点为抛物线上介于两点之间的一点，设抛物线在点处的切线与圆交于两点，在圆上是否存在点，使得直线均为抛物线的切线，若存在求出点坐标（用表示）；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分10分）选修4-4：坐标系与参数方程

    在直角坐标系xOy中，曲线的参数方程为为参数），M为上的动点，P点满足，点P的轨迹为曲线．

    （I）求的方程；

    （II）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线与的异于极点的交点为A，与的异于极点的交点为B，求|AB|．

    查看答案和解析>>

    同步练习册答案