
【题目】已知CD是等边三角形ABC的AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
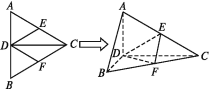
(1)求直线BC与平面DEF所成角的余弦值;
(2)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)以D为原点建立空间直角坐标系,设等边三角形ABC的边长为![]() ,可得直线BC的方向向量
,可得直线BC的方向向量![]() 和平面EDF的法向量
和平面EDF的法向量![]() =(3,-
=(3,-![]() ,3),设直线BC与平面DEF所成角为
,3),设直线BC与平面DEF所成角为![]() ,则有
,则有![]() ,然后再求出
,然后再求出![]() ,即为所求.(2)假设在线段BC上存在一点,使得AP⊥DE,则由
,即为所求.(2)假设在线段BC上存在一点,使得AP⊥DE,则由![]() =
=![]() 可得P
可得P![]() ,于是
,于是![]() ,由
,由![]() 可得
可得![]() ,符合题意,进而得到结论.
,符合题意,进而得到结论.
(1)以点D为坐标原点,直线DB,DC分别为x轴,y轴,建立空间直角坐标系,
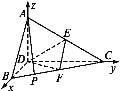
设等边三角形ABC的边长为a,则A![]() ,B
,B![]() ,C
,C![]() ,E
,E![]() ,F
,F![]() ,
,
设平面EDF的法向量为![]() ,
,
则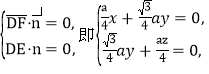
取![]() =(3,-
=(3,-![]() ,3).
,3).
又因为![]() ,
,
设直线BC与平面DEF所成角为![]() ,
,
则![]() ,
,
所以![]() ,
,
即直线BC与平面DEF所成角的余弦值等于![]() .
.
(2)假设在线段BC上存在一点,使AP⊥DE,
令![]() =
=![]() ,
,
即![]() =λ
=λ![]() ,
,
则P![]() ,
,
于是![]() .
.
因为AP⊥DE,
所以![]() ,
,
整理得![]() λa2-
λa2-![]() a2=0,
a2=0,
解得![]() ,符合题意.
,符合题意.
故线段BC上存在一点P,使AP⊥DE.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣ax+b(a>0,b>0)有两个不同的零点m,n,且m,n和﹣2三个数适当排序后,即可成为等差数列,也可成为等比数列,则a+b的值为( )
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)= ![]() ;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
A.①②
B.③④
C.①③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(I)已知函数f(x)=rx﹣xr+(1﹣r)(x>0),其中r为有理数,且0<r<1.求f(x)的最小值;
(II)试用(I)的结果证明如下命题:设a1≥0,a2≥0,b1 , b2为正有理数,若b1+b2=1,则a1b1a2b2≤a1b1+a2b2;
(III)请将(II)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.注:当α为正有理数时,有求导公式(xα)r=αxα﹣1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的导函数y=f'(x)的图像如图所示.

则下列说法中正确的是____(填序号).
①函数y=f(x)在区间![]() 上单调递增;
上单调递增;
②函数y=f(x)在区间![]() 上单调递减;
上单调递减;
③函数y=f(x)在区间(4,5)上单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x=-![]() 时,函数y=f(x)有极大值.
时,函数y=f(x)有极大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.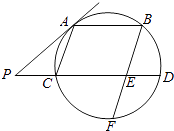
(1)求AC的长;
(2)试比较BE与EF的长度关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:
(1)BE=EC;
(2)ADDE=2PB2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}各项均为正数,其前n项和为Sn,且满足4Sn=(an+1)2.
(1)求{an}的通项公式;
(2)设![]() ,数列{bn}的前n项和为Tn,求Tn.
,数列{bn}的前n项和为Tn,求Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com