
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A= ![]() ,b2﹣a2=
,b2﹣a2= ![]() c2 .
c2 .
(1)求tanC的值;
(2)若△ABC的面积为3,求b的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设G为△ABC的重心,过G作直线l分别交线段AB,AC(不与端点重合)于P,Q.若 ![]() =λ
=λ ![]() ,
, ![]() =μ
=μ ![]() .
. 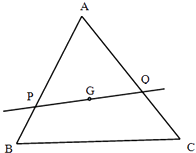
(1)求 ![]() 的值;
的值;
(2)求λμ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数{an}:a1=t,n2Sn+1=n2(Sn+an)+an2 , n=1,2,….
(1)设{an}为等差数列,且前两项和S2=3,求t的值;
(2)若t= ![]() ,证明:
,证明: ![]() ≤an<1.
≤an<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (k>0).
(k>0).
(1)若f(x)>m的解集为{x|x<﹣3或x>﹣2},求不等式5mx2+ ![]() x+3>0的解集;
x+3>0的解集;
(2)若存在x>3使得f(x)>1成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的个数是( )
①函数![]() 的零点有2个;
的零点有2个;
②函数![]() 的最小正周期是
的最小正周期是![]() ;
;
③命题“函数![]() 在
在![]() 处有极值,则
处有极值,则![]() ”的否命题是真命题;
”的否命题是真命题;
④![]() .
.
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了普及环保知识,增强环保意识,某校从理科甲班抽取60人,从文科乙班抽取50人参加环保知识测试.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
(Ⅰ)根据题目完成![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为环保知识成绩优秀与学生的文理分类有关.
的把握认为环保知识成绩优秀与学生的文理分类有关.
(Ⅱ)现已知![]() ,
, ![]() ,
, ![]() 三人获得优秀的概率分别为
三人获得优秀的概率分别为![]() ,
, ![]() ,
, ![]() ,设随机变量
,设随机变量![]() 表示
表示![]() ,
, ![]() ,
, ![]() 三人中获得优秀的人数,求
三人中获得优秀的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
附:  ,
, ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,且a1=2,a1+a2+a3=12.
(1)求数列{an}的通项公式;
(2)令bn=an3n(x∈R).求数列{bn}前n项和的公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过![]() 的动圆恒与
的动圆恒与![]() 轴相切,设切点为
轴相切,设切点为![]() 是该圆的直径.
是该圆的直径.
(Ⅰ)求![]() 点轨迹
点轨迹![]() 的方程;
的方程;
(Ⅱ)当![]() 不在y轴上时,设直线
不在y轴上时,设直线![]() 与曲线
与曲线![]() 交于另一点
交于另一点![]() ,该曲线在
,该曲线在![]() 处的切线与直线
处的切线与直线![]() 交于
交于![]() 点.求证:
点.求证: ![]() 恒为直角三角形.
恒为直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com