
【题目】.已知函数![]() .
.
(1)求过点![]() 的
的![]() 图象的切线方程;
图象的切线方程;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() ,
, ![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,均有
时,均有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)设切点坐标为![]() ,则切线方程为
,则切线方程为 ![]() ,根据点
,根据点![]() 坐标,即可求出
坐标,即可求出![]() ,从而得到切线方程;(2)对
,从而得到切线方程;(2)对![]() 求导,令
求导,令![]() ,要使
,要使![]() 存在两个极值点
存在两个极值点![]() ,
, ![]() ,则方程
,则方程![]() 有两个不相等的正数根,从而只需满足
有两个不相等的正数根,从而只需满足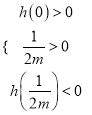 即可;(3)由
即可;(3)由![]() 在
在![]() 上恒成立可得
上恒成立可得![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,求出
,求出![]() 的单调性,可得出
的单调性,可得出![]() 的最大值,即可求得
的最大值,即可求得![]() 的取值范围.
的取值范围.
试题解析:(1)由题意得,函数![]() 的定义域为
的定义域为![]() ,
, ![]()
设切点坐标为![]() ,则切线方程为
,则切线方程为 ![]()
把点![]() 代入切线方程,得:
代入切线方程,得: ![]() ,
,
![]()
![]() 过点
过点![]() 的切线方程为:
的切线方程为: ![]()
(2)∵![]()
∴![]()
令![]()
要使![]() 存在两个极值点
存在两个极值点![]() ,
, ![]() ,则方程
,则方程![]() 有两个不相等的正数根.
有两个不相等的正数根.
又![]() ,
, ![]() .
.
故只需满足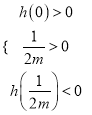 即可
即可
解得: ![]()
(3)由于![]() 在
在![]() 上恒成立.
上恒成立.
∴![]() 在
在![]() 上恒成立.
上恒成立.
令![]()
则![]()
当![]() 时,
时, ![]()
令![]() ,则
,则![]()
![]()
![]() 在
在![]() 上单调递增
上单调递增
又![]() ,
, ![]()
∴存在![]() 便得
便得![]() ,即
,即![]() ,
, ![]()
故当![]() 时,
时, ![]() ,此时
,此时![]()
当时![]() ,
, ![]() 此时
此时![]() .
.
故函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减
上递减
从而: ![]()
令![]() ,
, ![]()
则![]()
![]()
![]() 在上
在上![]() 单调递增,
单调递增,
∴![]()
故![]() .
.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() 的焦点为F1(–1、0),
的焦点为F1(–1、0),
F2(1,0).过F2作x轴的垂线l,在x轴的上方,l与圆F2:![]() 交于点A,与椭圆C交于点D.连结AF1并延长交圆F2于点B,连结BF2交椭圆C于点E,连结DF1.已知DF1=
交于点A,与椭圆C交于点D.连结AF1并延长交圆F2于点B,连结BF2交椭圆C于点E,连结DF1.已知DF1=![]() .
.

(1)求椭圆C的标准方程;
(2)求点E的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:
点,则翻折后的几何体中有如下描述:
①![]() 与
与![]() 所成角的正切值是
所成角的正切值是![]() ;
;
②![]() ;
;
③![]() 是
是![]() ;
;
④平面![]() 平面
平面![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角为30°.
所成角为30°.
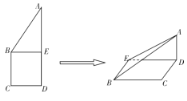
其中正确的有________.(填写你认为正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线的图象关于![]() 轴对称,顶点在坐标原点,点
轴对称,顶点在坐标原点,点![]() 在抛物线上.
在抛物线上.
(1)求抛物线的标准方程;
(2)设直线![]() 的方程为
的方程为![]() ,若直线
,若直线![]() 与抛物线交于
与抛物线交于![]() 两点,且以
两点,且以![]() 为直径的圆过点
为直径的圆过点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com