Question

【题目】已知等差数列{an}中，公差d>0，其前n项和为Sn，且满足：a2a3＝45，a1＋a4＝14.

(1)求数列{an}的通项公式；

(2)通过公式bn＝构造一个新的数列{bn}．若{bn}也是等差数列，求非零常数c；

(3)对于(2)中得到的数列{bn}，求f(n)＝ (n∈N*)的最大值．

Answer 1

【答案】(1)an＝4n－3．(2) ．

【解析】试题分析：

（1）由等差数列的性质可得a2＋a3＝14，解方程组可得a2＝5，a3＝9，于是可求得首项和公差，从而可得通项公式．（2）由题意得Sn＝2n2－n，故，根据数列为等差数列可得2b2＝b1＋b3，计算可得．经验证可得满足题意．（3）由（2）可得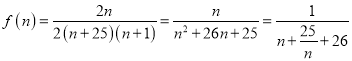，故可根据基本不等式求最值．

试题解析：

(1)∵数列{an}是等差数列．

∴a2＋a3＝a1＋a4＝14，

由，解得或．

∵公差d>0，

∴a2＝5，a3＝9．

∴d＝a3－a2＝4，a1＝a2－d＝1．

∴．

(2)∵Sn＝na1＋n(n－1)d＝n＋2n(n－1)＝2n2－n，

∴．

∵数列{bn}是等差数列，

∴2b2＝b1＋b3，

∴2·＝＋，

解得 (c＝0舍去)．

∴．

显然{bn}成等差数列，符合题意，

∴．

(3)由（2）可得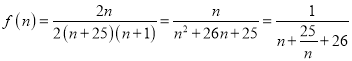

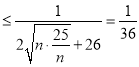，当且仅当，即时等号成立．

∴f(n)的最大值为．