
【题目】已知向量 ![]() =(1,0),
=(1,0), ![]() =(m,1),且
=(m,1),且 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() .
.
(1)求| ![]() ﹣2
﹣2 ![]() |;
|;
(2)若( ![]() +λ
+λ ![]() )与
)与 ![]() 垂直,求实数λ的值.
垂直,求实数λ的值.
【答案】
(1)解:∵ ![]() =(1,0),
=(1,0), ![]() =(m,1),且
=(m,1),且 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() .
.
∴ ![]() =m,|
=m,| ![]() |=1,|
|=1,| ![]() |=
|= ![]() ,
,
cos< ![]() >=
>= ![]() =
= ![]() ,解得m=1,或m=﹣1(舍)
,解得m=1,或m=﹣1(舍)
∴ ![]() =(﹣1,﹣2),
=(﹣1,﹣2),
∴| ![]() ﹣2
﹣2 ![]() |=
|= ![]() =
= ![]()
(2)解:∵ ![]() =(1+λ,λ),
=(1+λ,λ),
( ![]() +λ
+λ ![]() )与
)与 ![]() 垂直,
垂直,
∴ ![]() ,
,
解得 ![]()
【解析】(1)由cos< ![]() >=
>=  =
= ![]() ,求出m=1,由此能求出|
,求出m=1,由此能求出| ![]() ﹣2
﹣2 ![]() |.(2)由
|.(2)由 ![]() =(1+λ,λ),(
=(1+λ,λ),( ![]() +λ
+λ ![]() )与
)与 ![]() 垂直,能求出实数λ的值.
垂直,能求出实数λ的值.
【考点精析】本题主要考查了数量积表示两个向量的夹角和数量积判断两个平面向量的垂直关系的相关知识点,需要掌握设![]() 、
、![]() 都是非零向量,
都是非零向量,![]() ,
,![]() ,
,![]() 是
是![]() 与
与![]() 的夹角,则
的夹角,则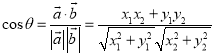 ;若平面
;若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直才能正确解答此题.
两平面的法向量垂直才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图是某工厂对甲乙两个车间各10名工人生产的合格产品的统计结果的茎叶图.设甲、乙的中位数分别为x甲、x乙 , 甲、乙的方差分别为s甲2、s乙2 , 则( ) 
A.x甲<x乙 , s甲2<s乙2
B.x甲>x乙 , s甲2>s乙2
C.x甲>x乙 , s甲2<s乙2
D.x甲<x乙 , s甲2>s乙2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①y=ax , ②y=bx , ③y=cx , ④y=dx , 根据图象可得a、b、c、d与1的大小关系为( )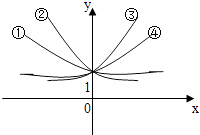
A.a<b<1<c<d
B.b<a<1<d<c
C.1<a<b<c<d
D.a<b<1<d<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知方程x2+ax+b=0.
(1)若方程的解集只有一个元素,求实数a,b满足的关系式;
(2)若方程的解集有两个元素分别为1,3,求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosx( ![]() sinx+cosx)+m,(x∈R,m∈R).
sinx+cosx)+m,(x∈R,m∈R).
(1)求f(x)的最小正周期;
(2)若f(x)在区间[0, ![]() ]上的最大值是6,求f(x)在区间[0,
]上的最大值是6,求f(x)在区间[0, ![]() ]上的最小值.
]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面为矩形,PA是四棱锥的高,PB与DC所成角为45°,F是PB的中点,E是BC上的动点.
(Ⅰ)证明:PE⊥AF;
(Ⅱ)若BC=2BE=2 ![]() AB,求直线AP与平面PDE所成角的大小..
AB,求直线AP与平面PDE所成角的大小..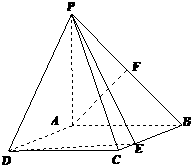
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点. 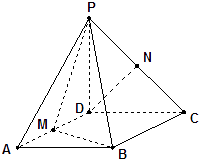
(1)证明:DN∥平面PMB;
(2)证明:平面PMB⊥平面PAD;
(3)求点A到平面PMB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com