
【题目】已知双曲线![]() 的离心率为2,
的离心率为2,![]() 分别是双曲线的左、右焦点,点
分别是双曲线的左、右焦点,点![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点,当
上的动点,当![]() 取得最小值和最大值时,
取得最小值和最大值时,![]() 的面积分别为
的面积分别为![]() ,则
,则![]() ____________.
____________.
【答案】![]()
【解析】
利用双曲线的离心率推出b=![]() a,线段MN所在直线的方程为y=
a,线段MN所在直线的方程为y=![]() (x+a),点P在线段MN上,可设P(m,
(x+a),点P在线段MN上,可设P(m,![]() (m+a)), 其中m∈[-a,0],由F1(-c,0),F2(c,0),通过斜率的数量积求出
(m+a)), 其中m∈[-a,0],由F1(-c,0),F2(c,0),通过斜率的数量积求出![]() 的最值,然后求解结果.
的最值,然后求解结果.
由已知e=![]() =2得c=2a,b=
=2得c=2a,b=![]() a,故线段MN所在直线的方程为y=
a,故线段MN所在直线的方程为y=![]() (x+a),又点P在线段MN上,可设P(m,
(x+a),又点P在线段MN上,可设P(m,![]() (m+a)),其中m∈[-a,0],由F1(-c,0),F2(c,0),得
(m+a)),其中m∈[-a,0],由F1(-c,0),F2(c,0),得![]() =(2am,
=(2am,![]() (m+a)),
(m+a)),![]() (2am,
(2am,![]() (m+a))),则
(m+a))),则![]() 4m2+6am
4m2+6am![]() ,由m∈[-a,0],可知当m=-
,由m∈[-a,0],可知当m=-![]() a时,
a时,![]() 取得最小值,此时S1=
取得最小值,此时S1=![]() ×2c×
×2c×![]() (-
(-![]() a+a)=
a+a)=![]() ac,当m=0时,
ac,当m=0时,![]() 取得最大值,此时S2=
取得最大值,此时S2=![]() ×2c×
×2c×![]() a=
a=![]()
ac,所以![]()
![]() .
.
故答案为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知x,y∈R,且 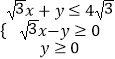 ,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]() ﹣
﹣ ![]()
C.![]()
D.![]() +
+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 点(n,Sn+3)(n∈N*)在函数y=3×2x的图象上,等比数列{bn}满足bn+bn+1=an(n∈N*).其前n项和为Tn , 则下列结论正确的是( )
A.Sn=2Tn
B.Tn=2bn+1
C.Tn>an
D.Tn<bn+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位打字员在两台电脑上各自输入A,B两种类型的文件的部分文字才能使这两类文件成为成品.已知A文件需要甲输入0.5小时,乙输入0.2小时;B文件需要甲输入0.3小时,乙输入0.6小时.在一个工作日中,甲至多只能输入6小时,乙至多只能输入8小时,A文件每份的利润为60元,B文件每份的利润为80元,则甲、乙两位打字员在一个工作日内获得的最大利润是元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|+|x+4|,g(x)=x2+4x+3.
(1)求不等式f(x)≥g(x)的解集;
(2)若f(x)≥|1﹣5a|恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分8分)某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.

(Ⅰ)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(Ⅱ)从测试成绩在[50,60)∪[90,100]内的所有学生中随机抽取两名同学,设其测试成绩分别为m、n,求事件“|m﹣n|>10”概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x>0),m∈R.
(x>0),m∈R.
(1)若函数f(x)有零点,求实数m的取值范围;
(2)若函数f(x)的图象在点(1,f(x))处的切线的斜率为 ![]() ,且函数f(x)的最大值为M,求证:1<M<
,且函数f(x)的最大值为M,求证:1<M< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅(公元前5~6世纪)是我国齐梁时代的数学家,是祖冲之的儿子.他提出了一条原理:“幂势既同,则积不容异.”这里的“幂”指水平截面的面积,“势”指高.这句话的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体体积相等.设由椭圆 ![]() =1(a>b>0)所围成的平面图形绕y轴旋转一周后,得一橄榄状的几何体(如图)(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于 .
=1(a>b>0)所围成的平面图形绕y轴旋转一周后,得一橄榄状的几何体(如图)(称为椭球体),课本中介绍了应用祖暅原理求球体体积公式的做法,请类比此法,求出椭球体体积,其体积等于 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax﹣lnx(a∈R,a为常数)
(1)当a=﹣1时,若方程f(x)= ![]() 有实根,求b的最小值;
有实根,求b的最小值;
(2)设F(x)=f(x)e﹣x , 若F(x)在区间(0,1]上是单调函数,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com