
【题目】已知x,y∈R,且  ,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
,则存在θ∈R,使得xcosθ+ysinθ+1=0成立的P(x,y)构成的区域面积为( )
A.4 ![]() ﹣
﹣ ![]()
B.4 ![]() ﹣
﹣ ![]()
C.![]()
D.![]() +
+ ![]()
【答案】A
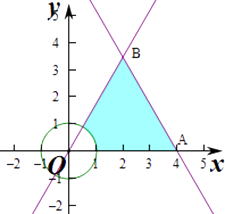
【解析】解:作出不等式组对应的平面区域如图:对应的区域为三角形OAB,
若存在θ∈R,使得xcosθ+ysinθ+1=0成立,
则 ![]() (
( ![]() cosθ+
cosθ+ ![]() sinθ)=﹣1,
sinθ)=﹣1,
令sinα= ![]() ,则cosθ=
,则cosθ= ![]() ,
,
则方程等价为 ![]() sin(α+θ)=﹣1,
sin(α+θ)=﹣1,
即sin(α+θ)=﹣ ![]() ,
,
∵存在θ∈R,使得xcosθ+ysinθ+1=0成立,
∴|﹣ ![]() |≤1,即x2+y2≥1,
|≤1,即x2+y2≥1,
则对应的区域为单位圆的外部,
由 ![]() ,解得
,解得 ![]() ,即B(2,2
,即B(2,2 ![]() ),
),
A(4,0),则三角形OAB的面积S= ![]() ×
× ![]() =4
=4 ![]() ,
,
直线y= ![]() x的倾斜角为
x的倾斜角为 ![]() ,
,
则∠AOB= ![]() ,即扇形的面积为
,即扇形的面积为 ![]() ,
,
则P(x,y)构成的区域面积为S=4 ![]() ﹣
﹣ ![]() ,
,
故选:A


科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥P﹣ABC的底面是等腰直角三角形,且∠ACB= ![]() ,侧面PAB⊥底面ABC,AB=PA=PB=2.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( )
,侧面PAB⊥底面ABC,AB=PA=PB=2.则这个三棱锥的三视图中标注的尺寸x,y,z分别是( ) 
A.![]() ,1,
,1, ![]()
B.![]() ,1,1
,1,1
C.2,1, ![]()
D.2,1,1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(ωx+φ)+cos(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为π,且f(﹣x)=f(x),则( )
)的最小正周期为π,且f(﹣x)=f(x),则( )
A.f(x)在(0, ![]() )单调递增
)单调递增
B.f(x)在( ![]() ,
, ![]() )单调递减
)单调递减
C.f(x)在( ![]() ,
, ![]() )单调递增
)单调递增
D.f(x)在( ![]() ,π)单调递增
,π)单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 
(Ⅰ)求证:AF∥平面PCE;
(Ⅱ)若二面角P﹣CD﹣B为45°,AD=2,CD=3,求点F到平面PCE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a﹣x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,AC=BC=2,∠ACB=90°,侧面PAB为等边三角形,侧棱 ![]() .
. 
(Ⅰ)求证:PC⊥AB;
(Ⅱ)求证:平面PAB⊥平面ABC;
(Ⅲ)求二面角B﹣AP﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2013年至2016年期间,甲每年6月1日都到银行存入m元的一年定期储蓄,若年利率为q保持不变,且每年到期的存款本息自动转为新的一年定期,到2017年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
A.m(1+q)4元
B.m(1+q)5元
C.![]() 元
元
D.![]() 元
元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的离心率为2,
的离心率为2,![]() 分别是双曲线的左、右焦点,点
分别是双曲线的左、右焦点,点![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点,当
上的动点,当![]() 取得最小值和最大值时,
取得最小值和最大值时,![]() 的面积分别为
的面积分别为![]() ,则
,则![]() ____________.
____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com